DeepLab v3

对于语义分割而言，下采样是必不可少的，首先 stride>1 的下采样层对于提升感受野非常重要，这样高层特征语义更丰富，而且对于分割来说较大的感受野也至关重要；另外的一个现实问题，没有下采样层，特征图一直保持原始大小，计算量是非常大的。

但为了得到高分辨率的特征，一般有两种方法，第一种是采用EncoderDecoder 结构，类似于U-NET结构，并且Decoder是一个渐进的过程，即要引入一个横向连接的部分，即引入低级特征增加空间信息特征分割准确度，横向连接可以通过 concat 或者 sum 操作来实现。第二种方法就是Atrous Convolution，减少下采样率但是又可以保证感受野

motivation

多尺度目标的分类问题
连续池化下采样导致的图像特征分辨率降低

contribution

空间金字塔模块，能在多个尺度探测卷积特征，并使用编码全局上下文的图像级特征进一步提高性能
使用膨胀卷积（dilated convolution）代替池化下采样，获取更密集的特征信息
提出了Multi Grid = (r1; r2; r3) 来表示膨胀率

architecture

首先使用级联的方式设计网络，连续使用下采样在更深的模块中获取远程信息，但连续的下采样会导致细节信息被忽略，所以使用膨胀卷积来获取图像的深层次信息，即修改分类网络的后面 block，用空洞卷积来替换 stride=2 的下采样层

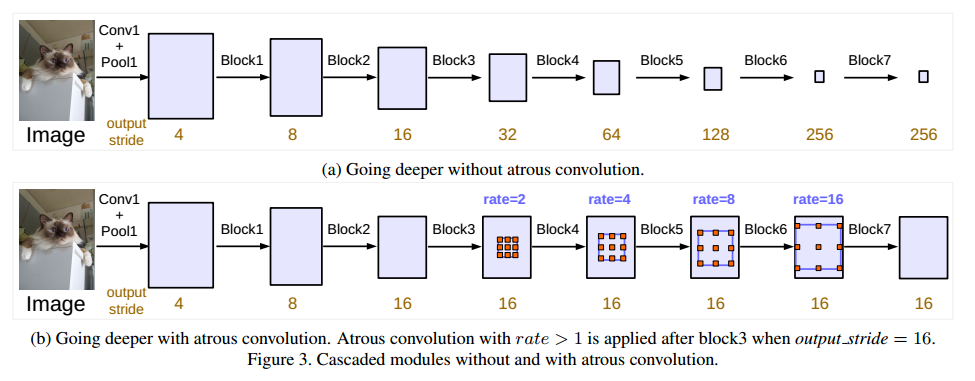
Block4将残差结构里的卷积层和捷径分支上的卷积层步距由2改为1，并且都改为膨胀卷积，这每个block里面有三个3*3的卷积，所以定义了Multi Grid = (r1; r2; r3) 来表示膨胀率，每个block的膨胀率等于rate * Multi Grid

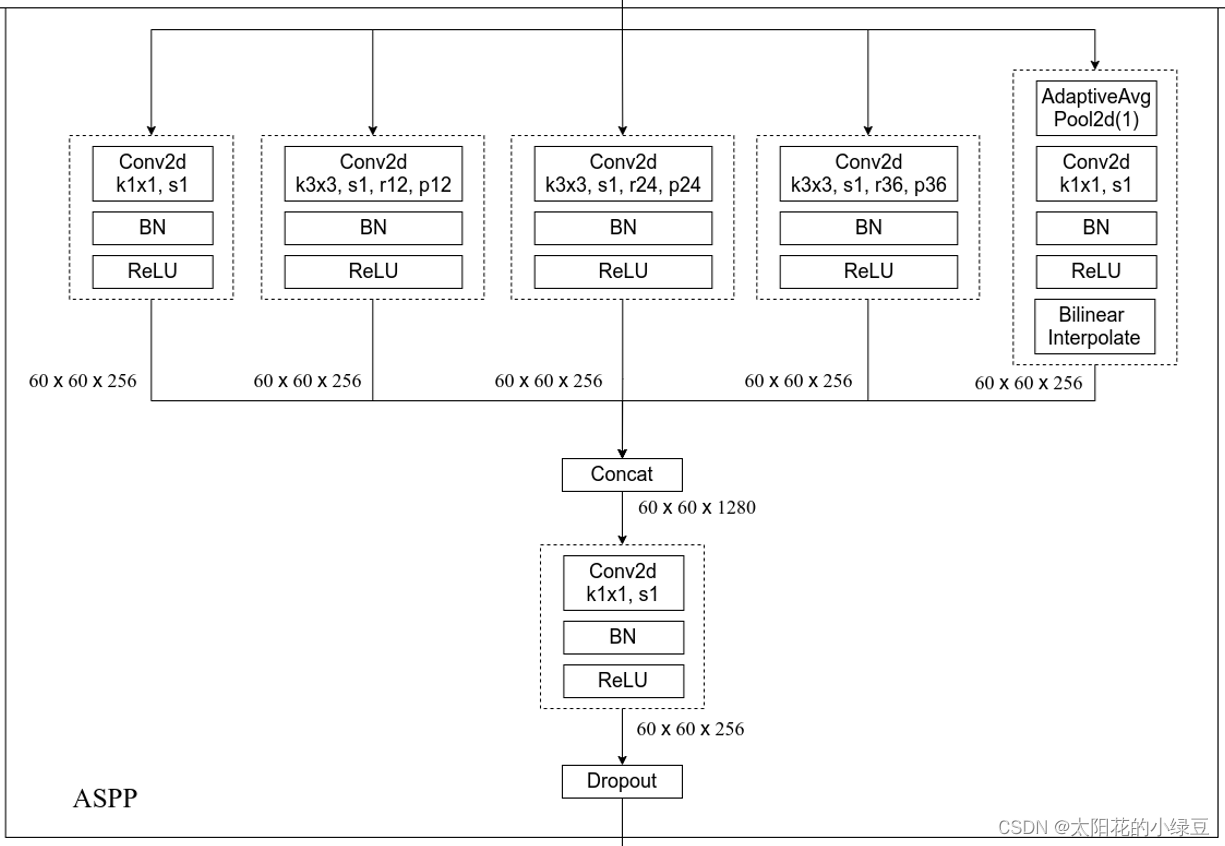
在不同尺度上重新采样特征对于准确有效地对任意尺度的区域进行分类是有效的，为了融合不同尺度的特征信息，作者又提出了ASPP模块

下图是使用3×3滤波器在一个65×65的特征图上进行卷积操作时，随着空洞率（atrous rate）的变化，有效权值的归一化计数也会发生变化。

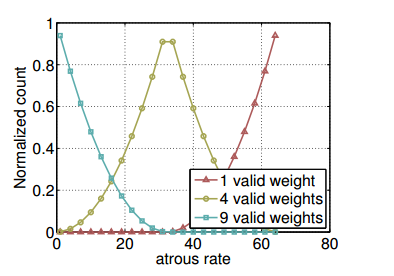
当空洞率比较小的时候，3*3滤波器的9个权值都比较有用，会应用于特征图上大部分有效区域，但随着空洞率增加，3×3滤波器会逐渐退化为一个1×1滤波器（当空洞率接近或超过特征图的大小时，滤波器的感受野已经扩展到整个特征图，就无法获取周围的信息）

这样会导致失去了对周围像素的重要信息捕捉能力，并且无法充分感知到整个图像的上下文信息，特别是对于距离中心像素较远的像素，上下文信息获取不足。

大概意思就是虽然较大的空洞率可以在一定程度上增加感受野（receptive field）并捕捉更大范围的上下文信息，但过大的空洞率会导致3×3滤波器效果退化为简单的1×1滤波器，从而引起信息损失和上下文不足的问题。在选择空洞率时，需要权衡考虑这些问题以及特定任务的需求。

为此作者提出了下面这个网络结构来解决上述问题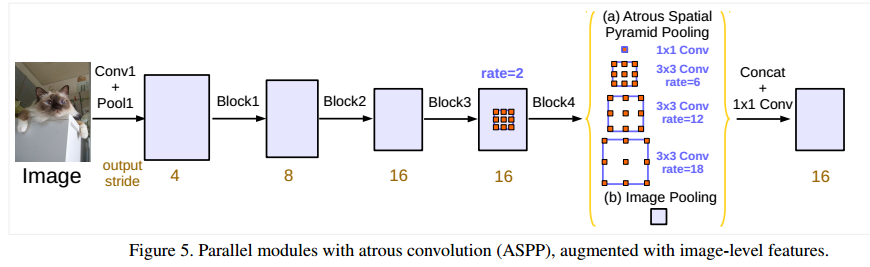

前面的都一样，当图像经过BLock4时，作者为了引入全局上下文信息，进行全局平均池化处理，然后将处理得到的图像级特征进行卷积操作和上采样，达到所需的空间维度，再与其他分支进行拼接，再经过卷积的得到最后的结果

下图是ASPP的详细结构，一共有五个分支，第一个分支是1*1的卷积层，我认为该分支的作用是修改上一层特征的维度，保留了上一层特征的信息，中间三个分支是使用了不同膨胀卷积系数的卷积层，最后一个是经历了全局池化的层，增加了全局信息，最后进行拼接，然后使用一个1 * 1的卷积层融合所有的信息。

class ASPP(nn.Module):
    def __init__(self, in_channels: int, atrous_rates: List[int], out_channels: int = 256) -> None:
        super(ASPP, self).__init__()
        modules = [
            # 第一个分支，1*1的卷积
            nn.Sequential(nn.Conv2d(in_channels, out_channels, 1, bias=False),
                          nn.BatchNorm2d(out_channels),
                          nn.ReLU())
        ]
        # 将膨胀卷积系数列表转化为元组的类型
        rates = tuple(atrous_rates)
        # 然后挨个遍历每一个膨胀系数，然后调用ASPPConv卷积
        for rate in rates:
            modules.append(ASPPConv(in_channels, out_channels, rate))

        modules.append(ASPPPooling(in_channels, out_channels))

        self.convs = nn.ModuleList(modules)

        self.project = nn.Sequential(
            nn.Conv2d(len(self.convs) * out_channels, out_channels, 1, bias=False),
            nn.BatchNorm2d(out_channels),
            nn.ReLU(),
            nn.Dropout(0.5)
        )

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        _res = []
        # 遍历convs里面的各个分支得到各自的结果，然后存入_res数组中
        for conv in self.convs:
            _res.append(conv(x))
        # 然后进行拼接
        res = torch.cat(_res, dim=1)
        return self.project(res)

为什么这样的结构能解决上面的问题，我总结了以下几个：

通过全局平均池化层，引入全局上下文信息
然后通过上采样操作，使其与其他特征具有相同的空间维度，进行有效的融合
采用了根据不同的输出步幅，使用不同的空洞率来扩大感受野

关于Multi Grid

作者试了很多种Multi Grid，发现在级联结构中，使用（1，2，1）效果是最好的

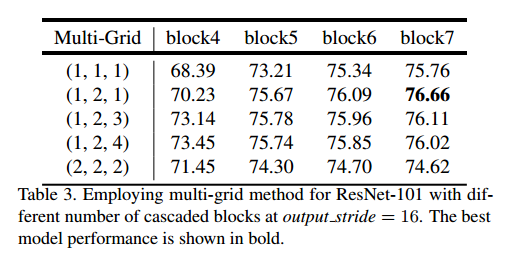
在使用ASPP的时候，发现Multi Grid使用（1，2，4）效果是最好的，并且高于使用级联结构，所以后续大多数实现都是使用ASPP这套结构

其他一些细节

在训练过程中增大了训练输入图片的尺寸（论文中有个观点大家需要注意下，即采用大的膨胀系数时，输入的图像尺寸不能太小，否则3x3的膨胀卷积可能退化成1x1的普通卷积。）
计算损失时，是将预测的结果通过上采样还原回原尺度后（即网络最后的双线性插值上采样8倍）在和真实标签图像计算损失。而之前在V1和V2中是将真实标签图像下采用8倍然后和没有进行上采样的预测结果计算损失（当时这么做的目的是为了加快训练）。根据Table 8中的实验可以提升一个多点。
训练后，冻结bn层的参数然后在fine-turn下网络，根据Table 8中的实验可以提升一个多点。

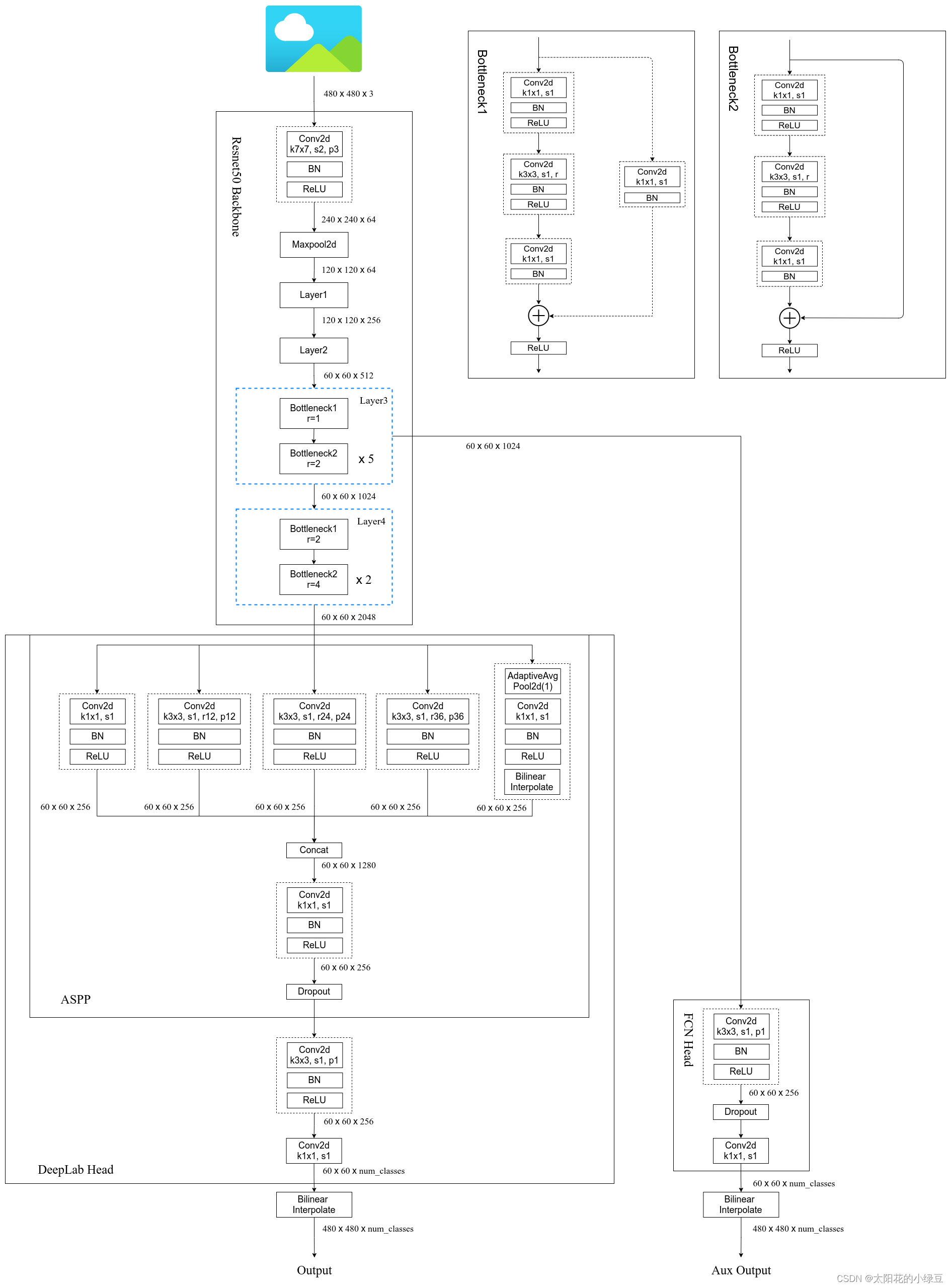
下图是Deeplab v3实现结构

请添加图片描述

DeepLab v3

semantic segmentation

DeepLab v3

motivation

contribution

architecture

CATALOG

FEATURED TAGS