swin transformer

motivation

图像变化很大，不固定
相较于文本信息，图像具有更大的分辨率，意味着计算复杂度要更大

contribution

利用分层结构来处理图像，使模型能够处理不同尺度的图片
使用window self-attention来降低计算复杂度

architecture

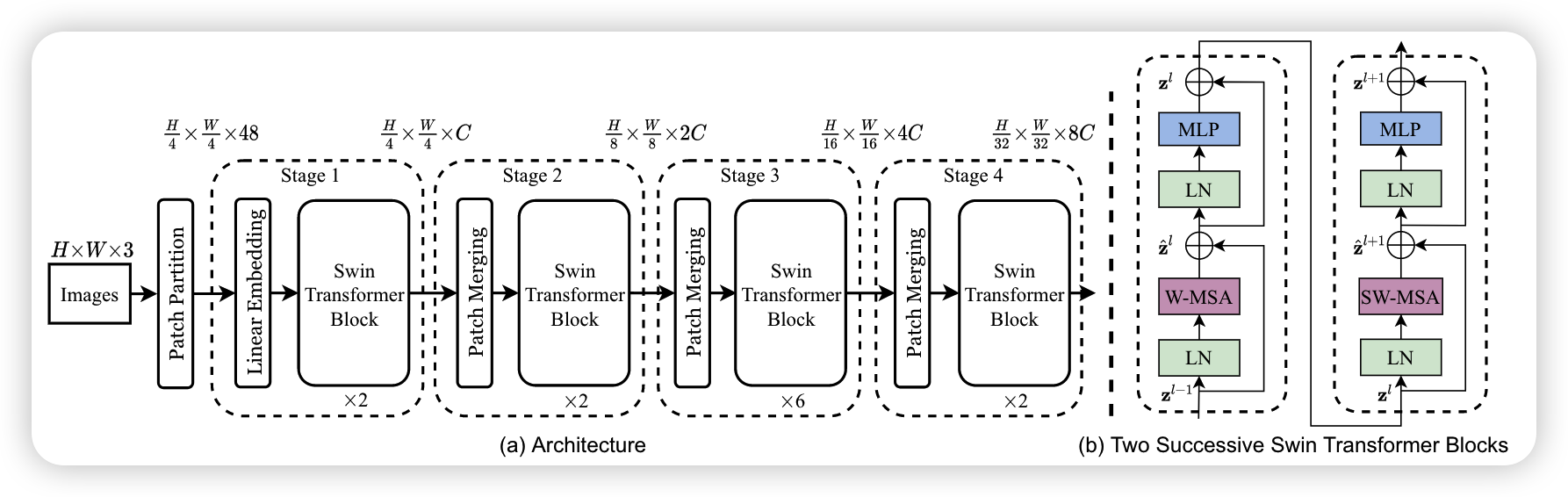
由上图可以看出基本流程如下：

首先将图片进入Patch Partition，将输入的特征图划分为一系列重叠的，固定大小的分块，从图中可以看出来长和宽缩小了四倍，所以每个分块大小是4*4个像素，然后在channel层进行展开，所以维度变成了16 * 3 =48，所以维度变为了[H/4 , W/4 , 48]，然后经过一个Linear Embedding将通道变为C
接着就是四个大致相同的stage模块，每个模块除了第一个都是Patch Merging+STB的结构，Patch Merging的作用是进行下采样，STB的作用是利用注意力机制，获取像素之间的联系信息，其结构如右图，包含两个结构，它们的区别在于一个使用的是W-MSA，一个使用的是SW-MSA

Patch Merging

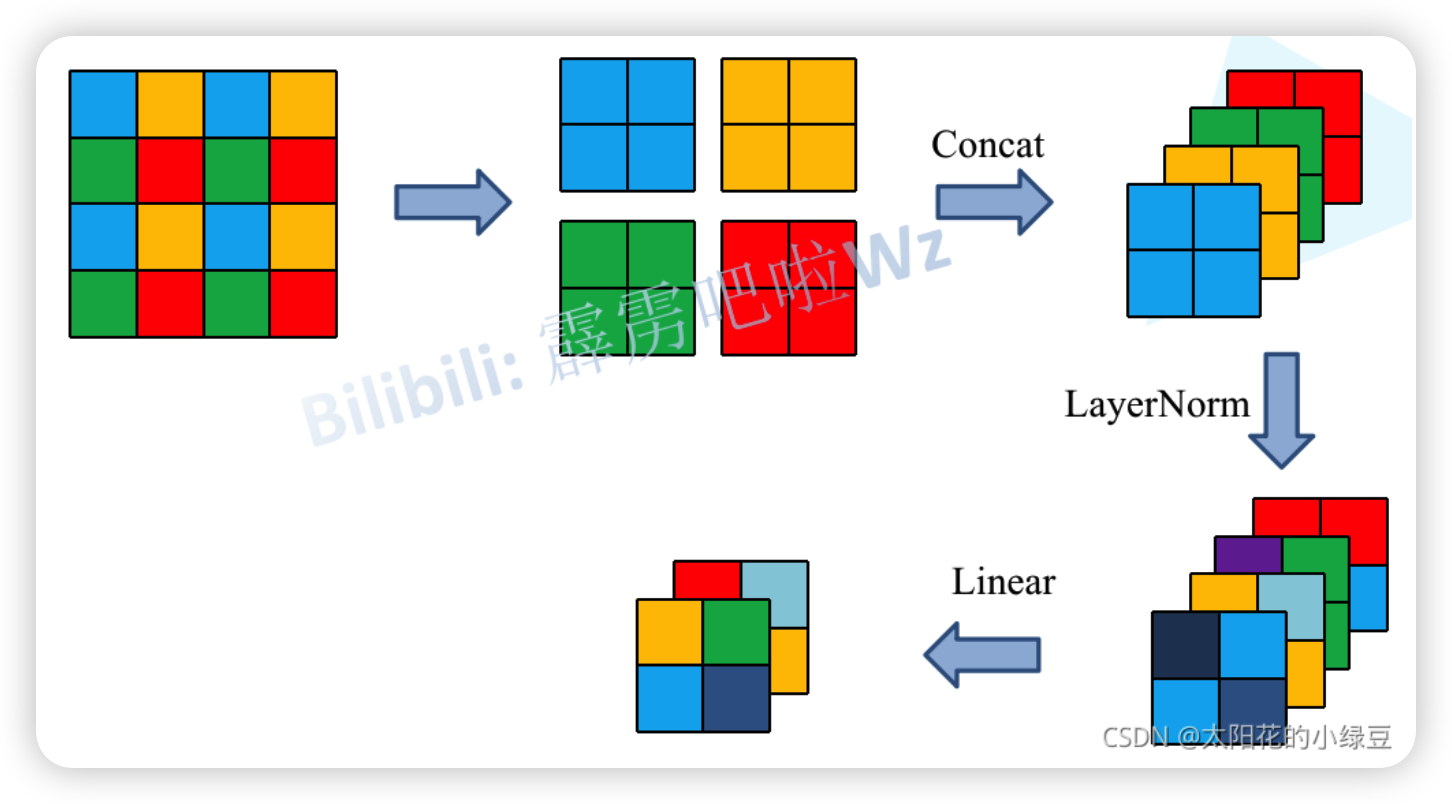
Patch Merging的作用是对图像进行下采样，和卷积网络中的pooling操作类似，下面是它的过程图，它首先会将输入特征图划分成多个2 * 2的patch图，然后提取每个patch中相同位置的像素然后拼接在一起，然后对这四个feature map进行concat操作，然后经过一个LayerNorm层，即标准化处理，最后经过一个Linear层调整通道数，这样得到的图像会从[H , W, C]——>[H/2 , W/2 , 2C]

class PatchMerging(nn.Module):
    r""" Patch Merging Layer.

    Args:
        dim (int): Number of input channels.
        norm_layer (nn.Module, optional): Normalization layer.  Default: nn.LayerNorm
    """
    def __init__(self, dim, norm_layer=nn.LayerNorm):
        super().__init__()
        self.dim = dim
        #创建全连接层
        self.reduction = nn.Linear(4 * dim, 2 * dim, bias=False)
        self.norm = norm_layer(4 * dim)

    def forward(self, x, H, W):
        """
        x: B, H*W, C
        """
        B, L, C = x.shape
        assert L == H * W, "input feature has wrong size"

        x = x.view(B, H, W, C)

        # padding
        # 如果输入feature map的H，W不是2的整数倍，需要进行padding
        pad_input = (H % 2 == 1) or (W % 2 == 1)
        if pad_input:
            # to pad the last 3 dimensions, starting from the last dimension and moving forward.
            # (C_front, C_back, W_left, W_right, H_top, H_bottom)
            # 注意这里的Tensor通道是[B, H, W, C]，所以会和官方文档有些不同
            x = F.pad(x, (0, 0, 0, W % 2, 0, H % 2))
        # 按照patch merging的过程抽出四个数组
        x0 = x[:, 0::2, 0::2, :]  # [B, H/2, W/2, C]
        x1 = x[:, 1::2, 0::2, :]  # [B, H/2, W/2, C]
        x2 = x[:, 0::2, 1::2, :]  # [B, H/2, W/2, C]
        x3 = x[:, 1::2, 1::2, :]  # [B, H/2, W/2, C]
        # 进行concat拼接
        x = torch.cat([x0, x1, x2, x3], -1)  # [B, H/2, W/2, 4*C]
        x = x.view(B, -1, 4 * C)  # [B, H/2*W/2, 4*C]
        #进行batchnorm
        x = self.norm(x)
        # 通过创建的全连接层，将4c转化为2c
        x = self.reduction(x)  # [B, H/2*W/2, 2*C]

        return x

Swin Transformer Block

W-MSA

W-MSA的结构大致和MSA的结构相似，区别在于W-MSA将特征图划分为一个个window，计算self-attention时只在window内部进行，这样会大大减少计算量，论文中给出了两者计算量之间的差距，公式如下

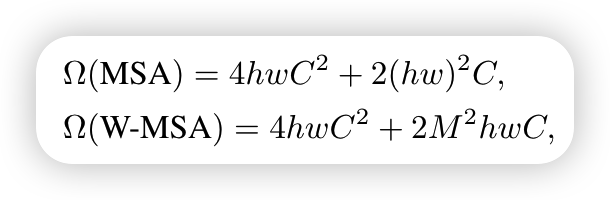
对于MSA的公式

首先是self-attention的计算公式如下

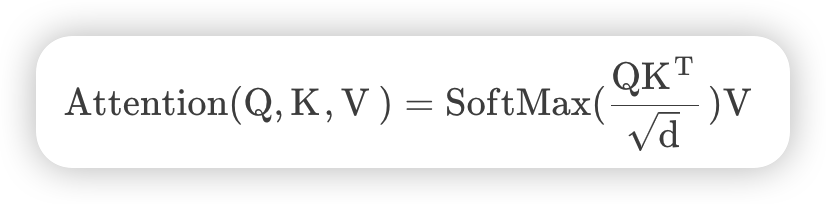
首先对于Q，K，V而言都是通过输入特征图与对应矩阵相乘得到的，输入特征图的维度是[h*w,c]，对应的矩阵维度是[c,c]，所以计算Q，K，V三个的复杂度为3 * h * w * c * c

Q（[h*w,c]）与K的转置（[c,h * w]）的积的复杂度为hw * c * hw，忽略除以d和softmax的计算量，最后与v相乘，复杂度为hw * hw * c，这是单头的self-attention的计算量，实际使用的是多头的self- attention，相比于单头的self-attention，计算量多了一个最后融合矩阵的计算，其计算量也是h * w *c *c，所以全部加起来为上面那个公式

对于W-MSA的公式

W-MSA是将特征图划分为一个个window，window的大小为M * M，个数为h/M * h/M，带入MSA的公式就可以得到W-MSA的计算量

SW-MSA

W-MSA虽然可以减少计算量，但缺点也是显而易见的，window与window之间没有联系，不能获取到全局的信息，为此引入了SW-MSA模块，进行偏移的W-MSA，如下图

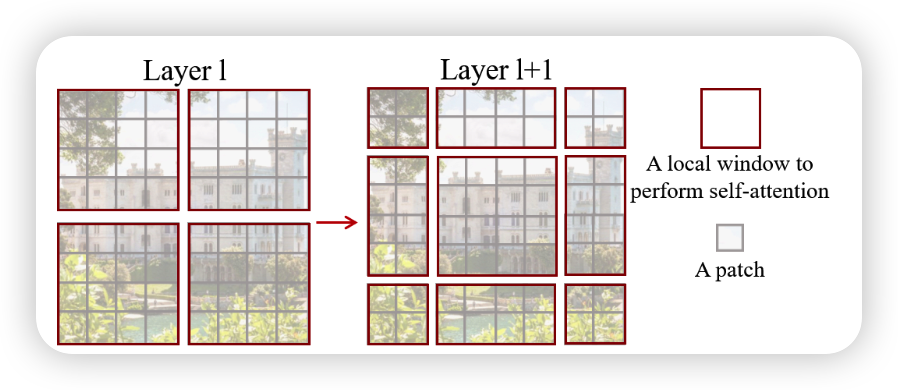
相当于将分界线向下，向右偏移[m/2]个像素，再重新融合得到右图，这样的好处在于将左图的不同window进行了融合，达到了不同window之间通信的效果，但这样做的坏处在于window从4个变为了9个，不利用并行计算，所以作者提出了cyclic shift方法，如下图所示

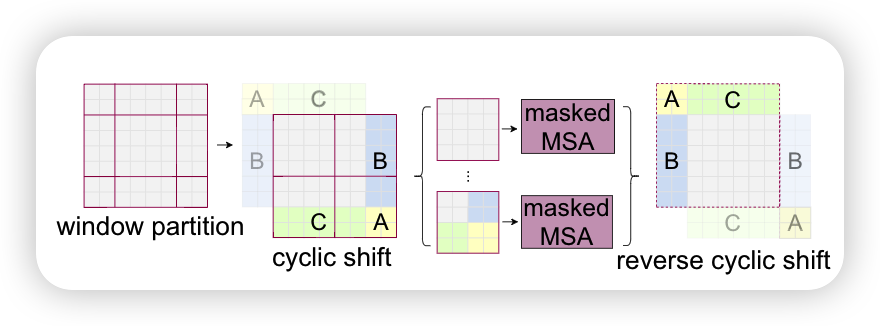
通过上图可以看出作者将边缘分块进行了位置上的调整，重新变为了4个window，但由于拼接的部分不是连续的，不适合放一起计算，所以虽然放在一个window中，但还是各自计算各自的，通过mask机制来实现，即在计算其中的一部分时，将另一部分减一个大的数，经过softmax之后这部分就会变为0，达到了mask的效果

def create_mask(self, x, H, W):
    # calculate attention mask for SW-MSA
    # 保证Hp和Wp是window_size的整数倍
    Hp = int(np.ceil(H / self.window_size)) * self.window_size
    Wp = int(np.ceil(W / self.window_size)) * self.window_size
    # 拥有和feature map一样的通道排列顺序，方便后续window_partition
    img_mask = torch.zeros((1, Hp, Wp, 1), device=x.device)  # [1, Hp, Wp, 1]
    # 将图像进行切片，按照shift来进行分割
    h_slices = (slice(0, -self.window_size),
                slice(-self.window_size, -self.shift_size),
                slice(-self.shift_size, None))
    w_slices = (slice(0, -self.window_size),
                slice(-self.window_size, -self.shift_size),
                slice(-self.shift_size, None))
    cnt = 0
    # 给不同的slices区域编号
    for h in h_slices:
        for w in w_slices:
            img_mask[:, h, w, :] = cnt
            cnt += 1
    # 将feature map按照window_size划分成一个个没有重叠的window 维度为[nW, Mh, Mw, 1]
    mask_windows = window_partition(img_mask, self.window_size)  # [nW, Mh, Mw, 1]
    # 将每一个window展平 
    mask_windows = mask_windows.view(-1, self.window_size * self.window_size)  # [nW, Mh*Mw]

    attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2)  # [nW, 1, Mh*Mw] - [nW, Mh*Mw, 1]
    # [nW, Mh*Mw, Mh*Mw] 通过相减，同区域的为0，赋值为0，不同区域的赋值-100
    attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0))
    return attn_mask

Relative position bias

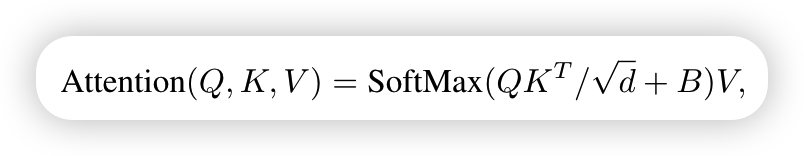
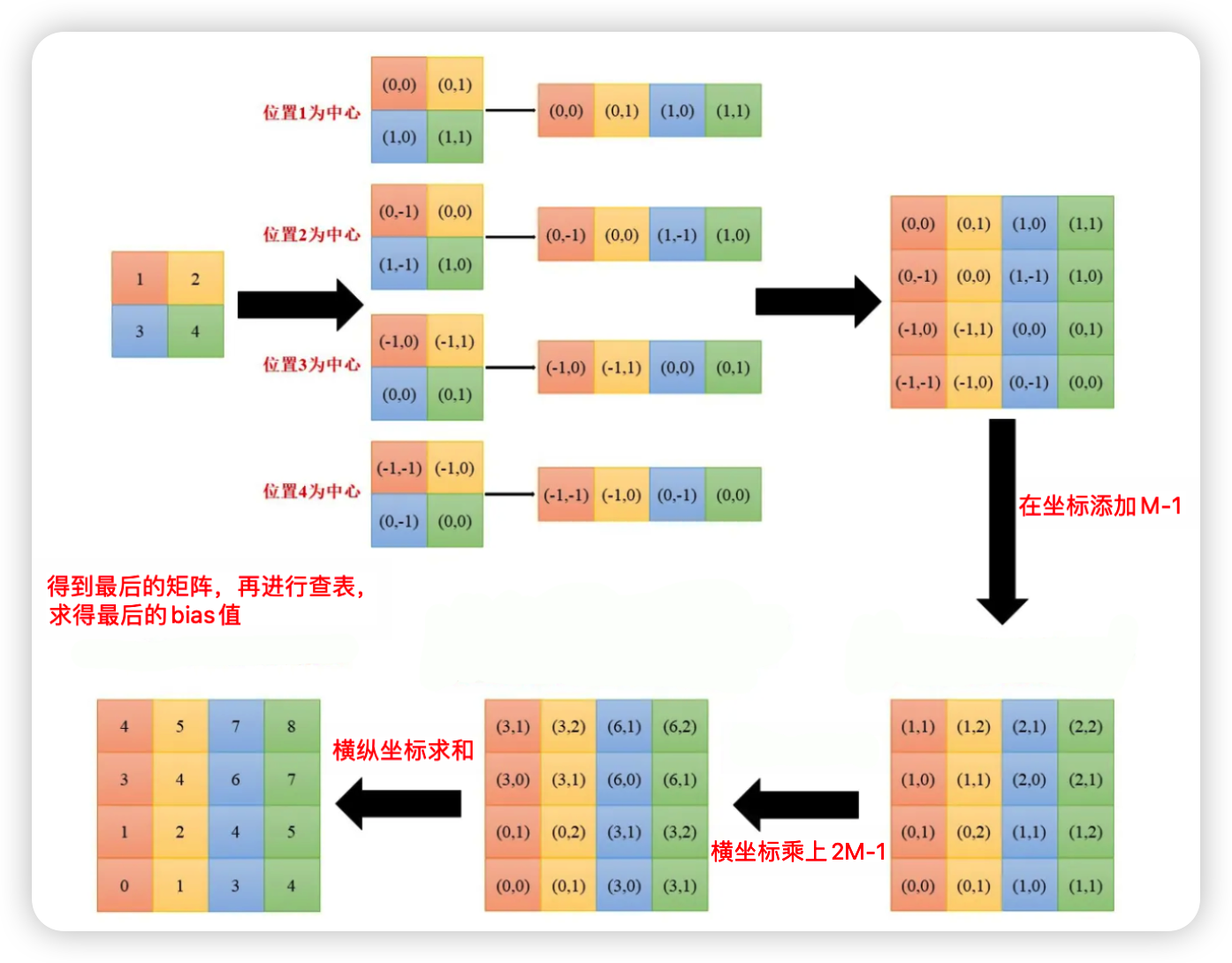
Bias计算过程

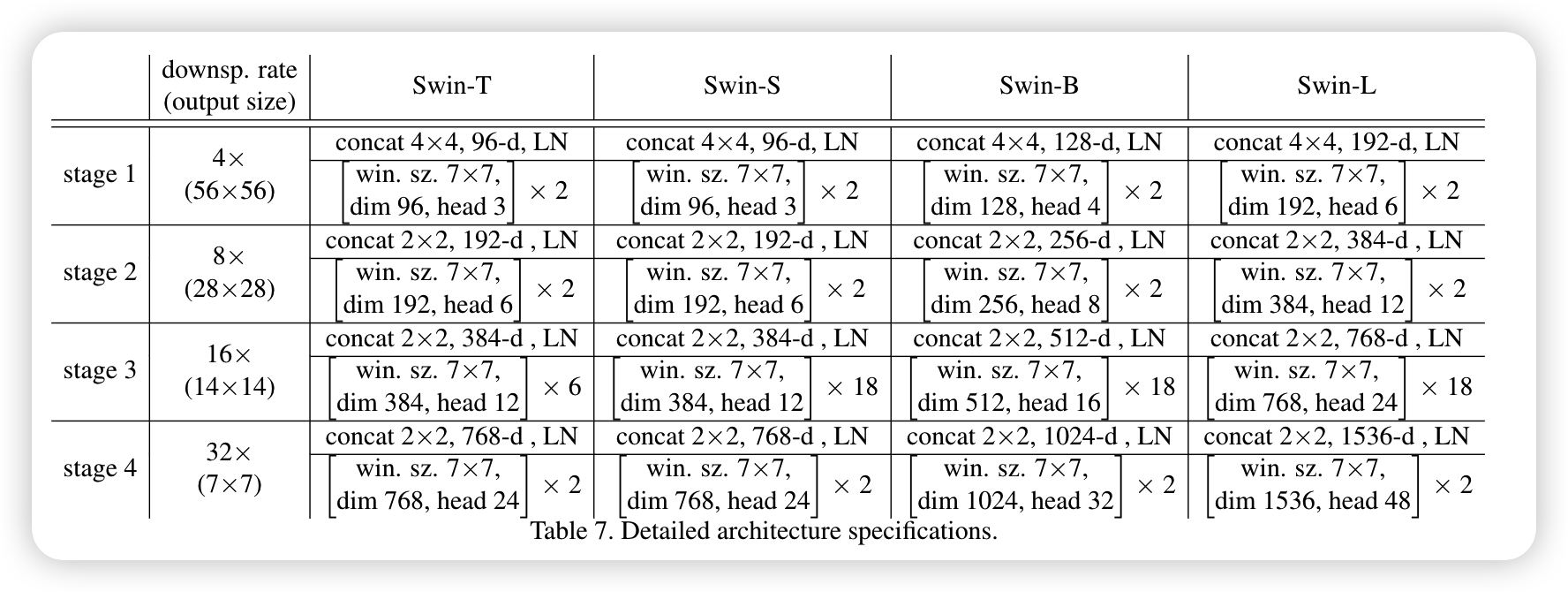
下表是论文中关于不同Swin Transformer的配置

参考

swin transformer

semantic segmentation