二分
格式
二分查找正确的编写姿势:
- 查找区间永远是闭区间[low,high]
- 循环条件永远是:low<=high
- 对于low–high的情况,必要的时候特殊处理,在while内部补充退出条件
- 返回值永远是mid,而不要是low,high
- low,high的更新永远是low=mid+1和high=mid-1
- 非确定性查找:对于非确定性查找,使用前后探测法,来确定搜索区间
- 先处理命中情况,再处理在左右半部分查找的请况 循环数组寻找最小值
非确定性查找:
- 第一个,最后一个相等的
- 第一个大于等于的,最后一个小于等于的
- 寻找峰值
例题
猜数字大小
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
* Forward declaration of guess API.
* @param num your guess
* @return -1 if num is higher than the picked number
* 1 if num is lower than the picked number
* otherwise return 0
* int guess(int num);
*/
public class Solution extends GuessGame {
public int guessNumber(int n) {
int left=1,right=n;
while(left<=right){
int mid=left+(right-left)/2;
if(guess(mid)==0)
return mid;
else if(guess(mid)>0){
left=mid+1;
}else{
right=mid-1;
}
}
return -1;
}
}
搜索插入位置
如果有则返回该位置,如果没有就返回应该插入的位置,但考虑二分查找的思路,如果没找到,那left和right的位置就应该是要插入的位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public int searchInsert(int[] nums, int target) {
int left=0,right=nums.length-1;
while(left<=right){
int mid=left+(right-left)/2;
if(nums[mid]==target){
return mid;
}else if(nums[mid]>target){
right=mid-1;
}else{
left=mid+1;
}
}
return left;
}
}
在排序数组中查找元素的第一个和最后一个位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
public int[] searchRange(int[] nums, int target) {
int left=getfirst(nums,target);
int right=getlast(nums,target);
return new int[]{left,right};
}
public int getfirst(int []nums,int target){
int left=0,right=nums.length-1;
while(left<=right){
int mid=left+(right-left)/2;
//先处理命中
if(nums[mid]==target){
//真命中 前后探测法确定搜索空间
if(mid==0||nums[mid-1]!=target)
return mid;
//伪命中
else
right=mid-1;
}else if(nums[mid]>target){
right=mid-1;
}else{
left=mid+1;
}
}
return -1;
}
public int getlast(int []nums,int target){
int left=0,right=nums.length-1;
while(left<=right){
int mid=left+(right-left)/2;
if(nums[mid]==target){
if(mid==nums.length-1||nums[mid+1]!=target){
return mid;
}else{
left=mid+1;
}
}else if(nums[mid]>target){
right=mid-1;
}else{
left=mid+1;
}
}
return -1;
}
}
寻找比目标字母大的最小字母
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public char nextGreatestLetter(char[] letters, char target) {
int left=0,right=letters.length-1;
while(left<=right){
int mid=left+(right-left)/2;
//处理命中 题目要求的是大于,那这里的判断条件就是大于
if(letters[mid]>target){
//真命中
if(mid==0||letters[mid-1]<=target)
return letters[mid];
else
right=mid-1;
}else{
left=mid+1;
}
}
return letters[0];
}
}
查找第一个大于等于x和最后一个小于等于x的数
一样的思路:前面的步骤一样,先处理命中情况,再处理不命中,在命中情况下处理真命中和伪命中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
public int[] searchRange(int[] nums, int target) {
int left=getfirst(nums,target);
int right=getlast(nums,target);
return new int[]{left,right};
}
public int getfirstge(int []nums,int target){
int n=nums.length;
int left=0,right=n-1;
while(left<=right){
int mid=left+(right-left)/2;
//先处理命中
if(nums[mid]>=target){
if(mid==0||nums[mid-1]<target){
return mid;
}else{
right=mid-1;
}
}else{
left=mid+1;
}
}
return -1;
}
public int getlastle(int []nums,int target){
int n=nums.length;
int left=0,right=n-1;
while(left<=right){
int mid=left+(right-left)/2;
if(nums[mid]<=target){
if(mid==n-1||nums[mid+1]>target){
return mid;
}else{
left=mid+1;
}
}else{
right=mid-1;
}
}
return -1;
}
}
循环有序数组查找目标
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public int[] searchX(int[] nums, int target) {
int n=nums.length;
int left=0,right=n-1;
while(left<=right){
int mid=left+(right-left)/2;
//先处理命中
if(nums[mid]==target){
return mid;
//再处理不命中
//找target在哪个区间
//首先就要判断哪个区间是有序的
}else if(nums[left]<=nums[mid]){
//左边有序
if(nums[left]<=target&&target<=nums[mid]){
right=mid-1;
}else{
left=mid+1;
}
}else{
//右边有序
if(nums[mid]<=target&&target<=nums[right]){
left=mid+1;
}else{
right=mid-1;
}
}
}
return -1;
}
}
循环有序数组查找最小值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public int findMin(int[] nums) {
int n=nums.length;
int left=0,right=nums.length-1;
while(left<=right){
int mid=left+(right-left)/2;
//特殊情况
if(left==right){
return nums[left];
}
//处理命中情况,即找最小值
if((mid!=0&&nums[mid-1]>nums[mid])
||(mid==0&&nums[mid]<nums[right]))
return nums[mid];
//处理非命中情况
//判断最小值归属区间
else if(nums[mid]<nums[right]){
right=mid-1;
}else
left=mid+1;
}
return -1;
}
}
山脉数组的峰顶索引
这道题题意说明了峰值是在数组中间,不会在边界处,所以在进行边界判断的时候直接越过,下道题就需要额外判断边界,使用compare方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public int peakIndexInMountainArray(int[] arr) {
int left=0,right=arr.length-1;
while(left<=right){
int mid=left+(right-left)/2;
if(mid==0)
left=mid+1;
else if(mid==arr.length-1)
right=mid-1;
//处理命中
else if(arr[mid]>arr[mid-1]&&arr[mid]>arr[mid+1])
return mid;
//处理非命中
//寻找分区
else if(arr[mid]<arr[mid+1]){
left=mid+1;
}else{
right=mid-1;
}
}
return -1;
}
}
查找峰值
思路不难,首先找命中,如果没有命中,就往这上坡的方向走即可,但这里要判断越界的情况,所以写了一个compare方法来帮助判断越界
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public int findPeakElement(int[] nums) {
int left=0,right=nums.length-1;
while(left<=right){
int mid=(left+right)/2;
//处理命中
if(compare(nums,mid-1,mid)<0&&compare(nums,mid,mid+1)>0)
return mid;
//处理非命中
//判断分区
if(compare(nums,mid,mid+1)<0){
left=mid+1;
}else{
right=mid-1;
}
}
return -1;
}
public int[]get(int []num,int index){
if(index==-1||index==num.length)
return new int[]{0,0};
return new int[]{1,num[index]};
}
public int compare(int []nums,int index1,int index2){
int[]num1=get(nums,index1);
int []num2=get(nums,index2);
if(num1[0]!=num2[0]){
return num1[0]>num2[0]?1:-1;
}
if(num1[1]==num2[1])
return 0;
return num1[1]>num2[1]?1:-1;
}
}
稀疏数组搜索
难点在于当索引到空字符串的时候,不知道往哪边移动,这个时候就可以用边界来判断,对边界进行移动
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public int findString(String[] words, String s) {
int left=0,right=words.length-1;
while(left<=right){
int mid=left+(right-left)/2;
if(words[mid].equals(s)){
return mid;
}else if(words[mid].equals("")){
//因为当位空的时候不知道往哪边动,所以用边界判断,让边界动,这样整体就又动起来了
if(words[left].equals(s))
return left;
else
left++;
}else if(words[mid].compareTo(s)<0){
left=mid+1;
}else{
right=mid-1;
}
}
return -1;
}
}
x 的平方根
求完全平方根,这是要求整数版
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public int mySqrt(int x) {
if(x==0)
return 0;
int left=0,riht=x/2+1;
while(left<=riht){
int mid=left+(riht-left)/2;
long product=(long)mid*mid;
if(product==x)
return mid;
else if(product>x){
riht=mid-1;
}else{
//存在
long product2=(long)(mid+1)*(mid+1);
if(product2<=x)
left=mid+1;
else
return mid;
}
}
return -1;
}
}
如果是要求平方根,并且要求保留5位小数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class Solution {
public double mySqrt(double x) {
if (x == 0) return 0;
double left = 0, right = x;
double epsilon = 0.000001; // 设置精度阈值
if (x < 1) {
right = 1;
}
while (right - left > epsilon) {
double mid = left + (right - left) / 2;
double square = mid * mid;
if (Math.abs(square - x) < epsilon) {
return mid; // 当差距小于epsilon时返回结果
} else if (square < x) {
left = mid;
} else {
right = mid;
}
}
return left + (right - left) / 2; // 取中值作为最终结果
}
}
有效的完全平方数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public boolean isPerfectSquare(int num) {
int left=0,right=num/2+1;
while(left<=right){
int mid=left+(right-left)/2;
long product=(long)mid*mid;
if(product==num)
return true;
else if(product<num){
long product2=(long)(mid+1)*(mid+1);
if(product2>num)
return false;
else
left=mid+1;
}else{
right=mid-1;
}
}
return false;
}
}
搜索二维矩阵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int i=matrix.length-1,j=0;
while(i>=0&&j<=matrix[0].length-1){
if(matrix[i][j]==target)
return true;
else if(matrix[i][j]>target){
i--;
}else{
j++;
}
}
return false;
}
}
动态规划
动态规划的题可以先想想回溯应该怎么做,然后找找重复子问题,翻译成动态规划
格式
动态规划解题过程
1.可用回溯解决:需要穷举搜索才能得到结果的问题(最值,可行,计数等)
2.构建多阶段决策模型。看是否能将问题求解的过程分为多个阶段。
3.查看是否存在重复子问题:是否有多个路径到达同一个状态。
4.定义状态:也就是如何记录每一阶段的不重复状态。
5.定义状态转移方程:也就是找到如何通过上一阶段的状态推导下一下阶段的状态。
6.画状态转移表:辅助理解,验证正确性,确定状态转移的初始值。
7.编写动态规划代码。
例如:
0-1背包问题
对于一组不同重量的物品,选择其中一些物品装入背包,在不超过背包最大重量限制的前提下,背包中可装物品总重量的最大值是多少? 1.可用回溯解决:穷举问题 2.构建多阶段决策模型:每一阶段决策一个物品是否放入背包 3.查看是否存在重复子问题:某一阶段背包中物品重量为cw,可以通过不同路径到达 4.定义状态: boolean dp[n][w+1]记录每一个阶段可达的所有状态。 dp[i][j]=true表示第i个物品决策完之后,存在背包中物品重量为j这种状态。 5.定义状态转移方程: 确定第i阶段的(i,j)这个状态,如何通过上一个阶段i-1的哪些状态转移过来
比如:(i,j)这个状态只有可能由(i-1,j)和(i-1,j-weight[i])转移过来,即dp[i][j]=dp[i-1][j] || dp[i-1][j-weight[i]]; 6.画状态转移表:辅助理解,验证正确性,确定状态转移的初始值。 7.编写动态规划代码
二维费用背包
对于一组不同重量, 不同价值的物品,选择其中某些物品装入背包,不超过背包最大重量限制的前提下,背包中可装入物品的总价值最大是多少? 1.可用回溯解决:穷举问题 2.构建多阶段决策模型:每一阶段决策一个物品是否放入背包 3.查看是否存在重复子问题:某一阶段背包中物,质量为cw,可以通过不同路径到达 4.定义状态: int dp[n][w+1]记录每一个阶段可达的所有状态, dp[i][j]可加表示第i个物品决策完之后,存在背包中物品重量为j,对应的最大物品价值 5.定义状态转移方程: 确定第i阶段的(i,j)这个状态,如何通过上一个阶段i-1的哪些状态转移过来 (i,j)这个状态只有可能由(i-1,j)和(i-1,j-weight[i])转移过来
即dp[i][j]=Math.max(dp[i-1][j] , dp[i-1][j-weight[i]]+value[i]) 6.画状态转移表:辅助理解,验证正确性,确定状态转移的初始值。 7.编写动态规划代码
定义状态转移方程
分为三种:最值、可行、计数
1、有n个物品,选择其中一些物品装入背包,在不超过背包最大重量限制的前提下,背包中可装物品总重量的最大值是多少?(最值) 状态: boolean dp[n][w+1]记录每一个阶段可达的所有状态。 dp[i][j]=true表示第i个物品决策完之后,存在背包中物品重量为j这种状态可达 状态转移方程: (i,j)这个状态只有可能由(i-1,j)和(i-1,j-weight[i])转移过来
| dp[i][j]=dp[i-1][j] | dp[i-1][j-weight[i]] |
2、有n个物品,选择其中一些物品装入背包,能不能正好装满背包? (可行) 状态: boolean dp[n][w+1]记录每一个阶段可达的所有状态。 dp[i][j]=true表示第i个物品决策完之后,存在背包中物品重量为j这种状态可达 状态转移方程: (i,j)这个状态只有可能由(i-1,j)和(i-1,j-weight[i])转移过来
| dp[i][j]=dp[i-1][j] | dp[i-1][j-weight[i]] |
3、有n个物品,选择其中一些物品装入背包,正好装满背包所需物品最少个数(如果装不满,返回-1)(最值) 状态: int dp[n][w+1]记录每个阶段可达重量对应最小物品个数。 dp[i][j]表示第i个物品决策完之后,背包中物品重量为j,对应的最小物品个数 状态转移方程: (i,j)这个状态只有可能由(i-1,j)和(i-1,j-weight[i])转移过来
dp[i][j]=Math.min(dp[i-1][j] , dp[i-1][j-weight[i]]+1)
4、有n个物品,选择其中一些物品装入背包,装满背包有多少种不同的装法?(计数) 状态: int dp[n][w+1]记录每个阶段可达重量对应装法个数。 dp[i][j]表示第i个物品决策完之后,背包中物品重量为j,对应的装法个数 状态转移方程: (i,j)这个状态只有可能由(i-1,j)和(i-1,j-weight[i])转移过来
dp[i][j]=dp[i-1][j] +dp[i-1][j-weight[i]]
背包
背包问题是选或者不选来凑成某个数,所以思路也是挨个遍历每一个i,选或者不选凑成j,最后来看遍历完求j=target时的值
问题背景
背包问题可以分为下面四类:
1)0-1背包问题 有n个物品,重量分别为weighti,每个物品只有一个,选择一些物品装入背包,在不超过背包总重量w的前提下,…. 2)完全背包问题 有n个物品,重量分别为weighti,每个物品有无限多个,选择一些物品装入背包,在不超过背包重量w的前提下,…. 3)多重背包问题 有n个物品,重量分别为weighti,每个物品有有限多个,个数分别为counti,选择一些物品装入背包,在不超过背包重量w的前提下,…. 4)二维费用 有n个物品,重量分别为weighti,价值分别为valuei,在不超过背包重量w的前提下,装入背包物品的最大价值是多少? 在上面的1)2)3)个背景下,可能需要求解的问题:
a)背包可装物品总重量的最大值是多少?
b)是否能装满整个背包?
c)正好装满背包最少需要多少物品?
d)装满背包有多少种装法?
各类解法
1)0-1背包问题
0-1背包:每个阶段决策一个物品是否装入背包,0个或1个
a)背包可装物品总重量的最大值是多少?可达性问题 状态: boolean dp[n][w+1]记录每阶段可达状态。 dp[i][j]=true表示第i个物品决策完之后,背包重量为j这个状态可达。 状态转移方程: (i,j)这个状态只有可能从(i-1,j)和(i-1,j-weight[i])两个状态转移过来 dp[i][j]=dp[i-1][j] || dp[i-1][j-weight[i]]
b)是否能装满整个背包? 和上一个的区别在于返回w是否为true 可达性问题
状态: boolean dp[n][w+1]记录每阶段可达状态。 dp[i][j]=true表示第i个物品决策完之后,背包重量为j这个状态可达。 状态转移方程: (i,j)这个状态只有可能从(i-1,j)和(i-1,j-weight[i])两个状态转移过来 dp[i][j]=dp[i-1][j] || dp[i-1][j-weight[i]]
c)正好装满背包最少需要多少物品? 最值问题
状态: int dp[n][w+1]表示每个阶段,可达重量最少物品个数是多少 dp[i][j]表示第i个物品决策完之后,背包重量为j,对应的最少物品个数。 状态转移方程: (i,j)这个状态只有可能从(i-1,j)和(i-1,j-weight[i])两个状态转移过来 dp[i][j]=Math.min(dp[i-1][j] ,dp[i-1][j-weight[i]]+1)
d)装满背包有多少种装法? 计数问题
状态: int dp[n][w+1]表示每个阶段,可达重量的装法 dp[i][j]表示第i个物品决策完之后,背包重量为j,对应的装法。 状态转移方程: (i,j)这个状态只有可能从(i-1,j)和(i-1,j-weight[i])两个状态转移过来 dp[i][j]=dp[i-1][j] +dp[i-1][j-weight[i]]
2)完全背包问题
和0-1的区别在于物品可以无限个,所以只有转移过来的状态有区别
a)背包可装物品总重量的最大值是多少? 可达性问题 状态: boolean dp[n][w+1]记录每阶段可达状态。 dp[i][j]=true表示第i个物品决策完之后,背包重量为j这个状态可达。 状态转移方程: (i,j)这个状态只有可能从(i-1,j)和(i,j-weight[i])两个状态转移过来 dp[i][j]=dp[i-1][j] || dp[i][j-weight[i]]
b)是否能装满整个背包? 和上一个的区别在于返回w是否为true 可达性问题
状态: boolean dp[n][w+1]记录每阶段可达状态。 dp[i][j]=true表示第i个物品决策完之后,背包重量为j这个状态可达。 状态转移方程: (i,j)这个状态只有可能从(i-1,j)和(i,j-weight[i])两个状态转移过来 dp[i][j]=dp[i-1][j] || dp[i][j-weight[i]]
c)正好装满背包最少需要多少物品? 最值问题
状态: int dp[n][w+1]表示每个阶段,可达重量最少物品个数是多少 dp[i][j]表示第i个物品决策完之后,背包重量为j,对应的最少物品个数。 状态转移方程: (i,j)这个状态只有可能从(i-1,j)和(i,j-weight[i])两个状态转移过来 dp[i][j]=Math.min(dp[i-1][j] ,dp[i][j-weight[i]]+1)
d)装满背包有多少种装法? 计数问题
状态: int dp[n][w+1]表示每个阶段,可达重量的装法 dp[i][j]表示第i个物品决策完之后,背包重量为j,对应的装法。 状态转移方程: (i,j)这个状态只有可能从(i-1,j)和(i,j-weight[i])两个状态转移过来 dp[i][j]=dp[i-1][j] +dp[i][j-weight[i]]
这里有个小技巧,最值和可达问题初始化的时候都是设置的不可达,计数问题初始化的时候是0
3)多重背包问题
和完全背包问题的区别在于每个阶段可以试的个数是不一样的
以计数问题为例,多了一层for循环,这个循环的k是最多能放多少个i和i的个数求最小值,接着dp[i][j]就对这些情况求和即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public int change(int amount, int[] coins, int []count) {
int[][]dp=new int[coins.length+1][amount+1];
dp[0][0]=1;
for(int i=1;i<=coins.length;i++){
for(int j=0;j<=amount;j++){
int k=Math.min(count[i-1],j/coins[i-1]);
for(int c=0;c<=k;c++){
dp[i][j]+=dp[i-1][j-c*coins[i-1]];
}
}
}
return dp[coins.length][amount];
}
}
4)二维费用
状态: int dp[n][w+1]表示每个阶段可达的所有状态 dp[i][j]表示第i个物品决策完之后,背包重量为j,对应的最大价值。 状态转移方程: (i,j)这个状态只有可能从(i-1,j)和(i-1,j-weight[i])两个状态转移过来 dp[i][j]=Math.max(dp[i-1][j] ,dp[i-1][j-weight[i]]+value[i-1])
分割等和子集
0-1背包的可达性问题,题意就是判断数组中元素是否能组合成sum的一半,这和0-1背包问题是一样的,所以思路就是把所有能达到的j都达到,最后判断在一半位置的j是否是可达的即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public boolean canPartition(int[] nums) {
int sum=0;
int target;
for(int n:nums)
sum+=n;
if(sum%2!=0)
return false;
target=sum/2;
//判断能不能达到,所以用boolean类型即可
boolean [][]dp=new boolean[nums.length+1][sum+1];
//初始化第0行
dp[0][0]=true;
//通过状态转移方程修改其余的位置
for(int i=1;i<=nums.length;i++){
for(int j=0;j<=sum;j++){
if(j-nums[i-1]<0){
dp[i][j]=dp[i-1][j];
}else{
if(dp[i-1][j]||dp[i-1][j-nums[i-1]])
dp[i][j]=true;
}
}
}
//判断目标位置即可
return dp[nums.length][target];
}
}
目标和
0-1背包计数问题,题意是统计到target的个数,想到用动态规划是因为每个数字就只有两种状态,一种是正,一种是负,所以可以默认首先是全为负的,那对于一个数来说,就一种不变或者变为正,两种状态
首先定义状态:dp[i][j]表示当轮到第i个数,数组和为j的个数,因为是有负的部分,所以0-sum-1表示负的部分,sum+1到2*sum表示正的部分
状态转移方程:dp[i][j]=dp[i-1][j]+dp[i-1][j-2*nums[i-1]]
最后返回的是和为target的,所以要找target的位置sum+target
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public int findTargetSumWays(int[] nums, int target) {
int sum=0;
for(int n:nums)
sum+=n;
if(target>sum||target<-sum)
return 0;
int [][]dp=new int[nums.length+1][2*sum+1];
dp[0][0]=1;
for(int i=1;i<=nums.length;i++){
for(int j=0;j<=2*sum;j++){
if(j-2*nums[i-1]<0){
dp[i][j]=dp[i-1][j];
}else{
dp[i][j]=dp[i-1][j]+dp[i-1][j-2*nums[i-1]];
}
}
}
return dp[nums.length][sum+target];
}
}
零钱兑换
完全背包最值问题,每种零钱的数量是无限的
首先定义状态:dp[i][j]表示当轮到第i个硬币时,目前凑齐数为j时需要的最少硬币数量
状态转移方程:dp[i][j]=Math.min(dp[i-1][j],dp[i][j-coins[i-1]]+1),因为这道题是要求全局最小,和上道题不一样,这是要比较凑的硬币数量最少。因为硬币数量是无限的,所以比较的时候是用不加这个硬币和再加一块硬币进行比较
这里因为是用了min函数,所以要将整个dp都初始化为amount+1(不可达)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public int coinChange(int[] coins, int amount) {
if(coins.length==1){
return amount%coins[0]==0?amount/coins[0]:-1;
}
int [][]dp=new int[coins.length+1][amount+1];
for(int []d:dp){
Arrays.fill(d,amount+1);
}
dp[0][0]=0;
for(int i=1;i<=coins.length;i++){
for(int j=0;j<=amount;j++){
if(j<coins[i-1]){
dp[i][j]=dp[i-1][j];
}else{
dp[i][j]=Math.min(dp[i-1][j],dp[i][j-coins[i-1]]+1);
}
}
}
return dp[coins.length][amount]==amount+1?-1:dp[coins.length][amount];
}
}
零钱兑换 II
完全背包计数问题,这道题思路和目标和一样
所以这里的状态方程dp[i][j]=dp[i-1][j]+dp[i][j-coins[i-1]],加的是dp[i][j-coins[i-1]],表示差少一个第i硬币的种数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public int change(int amount, int[] coins) {
int[][]dp=new int[coins.length+1][amount+1];
dp[0][0]=1;
for(int i=1;i<=coins.length;i++){
for(int j=0;j<=amount;j++){
if(j<coins[i-1]){
dp[i][j]=dp[i-1][j];
}else{
dp[i][j]=dp[i-1][j]+dp[i][j-coins[i-1]];
}
}
}
return dp[coins.length][amount];
}
}
路径问题
动态规划就路径问题有个特点是只能向下走和向右走,这便于进行遍历,如果是四个方向就是回溯
基本思路是首先遍历两条边界,两条边界的值是固定的,对于其他位置的值就根据题意来进行求最值或者相加
最小路径和
对于第0行和第0列来说,他们的值是固定死的,对于其他的位置来说,他们的值可以等于从左边过来或者从上面过来,那么就对其进行比较,求最小值即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public int minPathSum(int[][] grid) {
int[][]dp=new int[grid.length][grid[0].length];
dp[0][0]=grid[0][0];
for(int i=1;i<grid.length;i++){
dp[i][0]=dp[i-1][0]+grid[i][0];
}
for(int j=1;j<grid[0].length;j++){
dp[0][j]=dp[0][j-1]+grid[0][j];
}
for(int i=1;i<grid.length;i++){
for(int j=1;j<grid[0].length;j++){
dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+grid[i][j];
}
}
return dp[grid.length-1][grid[0].length-1];
}
}
礼物的最大价值
和上题思路一样,区别在于上题求min,这题求max
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public int jewelleryValue(int[][] frame) {
int m=frame.length;
int n=frame[0].length;
int[][]dp=new int[m][n];
dp[0][0]=frame[0][0];
for(int i=1;i<m;i++)
dp[i][0]=dp[i-1][0]+frame[i][0];
for(int j=1;j<n;j++)
dp[0][j]=dp[0][j-1]+frame[0][j];
for(int i=1;i<m;i++){
for(int j=1;j<n;j++){
dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1])+frame[i][j];
}
}
return dp[m-1][n-1];
}
}
三角形最小路径和
这道题和上道题思路一样,只不过是第0列和对角线的值是固定的,接着进行判断求最值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int n=triangle.size();
int [][]dp=new int[n][n];
dp[0][0]=triangle.get(0).get(0);
for(int i=1;i<n;i++){
dp[i][0]=dp[i-1][0]+triangle.get(i).get(0);
dp[i][i]=dp[i-1][i-1]+triangle.get(i).get(triangle.get(i).size()-1);
}
for(int i=2;i<n;i++){
for(int j=1;j<i;j++){
dp[i][j]=Math.min(dp[i-1][j-1],dp[i-1][j])+triangle.get(i).get(j);
}
}
int min=Integer.MAX_VALUE;
for(int i=0;i<n;i++){
if(dp[n-1][i]<min)
min=dp[n-1][i];
}
return min;
}
}
不同路径
这道题和上题的区别在于不是求路径上的值,而是求条数,所以对于第0列和第0行都是1,没有叠加,因为只是一条路径
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public int uniquePaths(int m, int n) {
int[][]dp=new int[m][n];
for(int i=0;i<m;i++)
dp[i][0]=1;
for(int j=1;j<n;j++)
dp[0][j]=1;
for(int i=1;i<m;i++){
for(int j=1;j<n;j++)
dp[i][j]=dp[i-1][j]+dp[i][j-1];
}
return dp[m-1][n-1];
}
}
不同路径 II
和上题思路一样,只不过加了障碍,对于第0行和第0列来说,障碍之后的都为0,对于其他区域,如果是障碍就为0,如果不是障碍就dp[i][j]=dp[i-1][j]+dp[i][j-1];
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
if(obstacleGrid[0][0]==1)
return 0;
int m=obstacleGrid.length,n=obstacleGrid[0].length;
int[][]dp=new int[m][n];
for(int i=0;i<m;i++){
if(obstacleGrid[i][0]==1)
break;
dp[i][0]=1;
}
for(int j=1;j<n;j++){
if(obstacleGrid[0][j]==1)
break;
dp[0][j]=1;
}
for(int i=1;i<m;i++){
for(int j=1;j<n;j++){
if(obstacleGrid[i][j]!=1)
dp[i][j]=dp[i-1][j]+dp[i][j-1];
else
dp[i][j]=0;
}
}
return dp[m-1][n-1];
}
}
打家劫舍 & 买卖股票
前后两个阶段是有牵制关系的,所以需要有一维作为状态设置,通过上一个阶段推测不同决策的最优解
这类问题都是选与不选,后一个阶段求选与不选的时候,就根据前一个阶段的选与不选求最优,将所有阶段的所有状态都更新一次
对于这类问题,首先找到不可达状态,设置为-Inf,对于一般的题只有第-1天的持有状态是不可达的,像股票买卖Ⅲ、Ⅳ,因为多了一个限制交易次数,所以要新增一个维度,多一层for循环,交易次数不可能为负的,所以要设置为不可达,其他的都一样
打家劫舍
这道题设置的规则在于不能取连续的,这不像背包问题,背包问题是可以连续也可以不连续,所以就不需要考虑这个问题,每次只需要考虑要不要加自己即可。这类题因为需要考虑,所以需要设置一个状态数组,表示每一个数的两种状态,因为后面的dp是需要用到前面的状态的
具体步骤如下:
1、构建多阶段决策模型 n个房屋对应n个阶段,每个阶段决定一个房屋偷还是不偷,两种决策:偷,不偷 2、定义状态 不能只记录每个阶段决策完之后,小偷可偷的最大金额,需要记录不同决策对应的最大金额,也就是:这个房屋偷-对应的最大金额;这个房屋不偷-对应的最大金额 int dp[n][2]记录每个阶段的状态 dp[i][0]:表示第i个物品不偷,当下的最大金额 dp[i][1]:表示第i个物品偷,当下的最大金额 3、定义状态转移方程 dp[i][0]=Math.max(dp[i-1][1],dp[i-1][0])
dp[i][1]=dp[i-1][0]+nums[i]
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public int rob(int[] nums) {
int n=nums.length;
int [][]dp=new int[n+1][2];
dp[0][1]=Integer.MIN_VALUE;
for(int i=1;i<=n;i++){
dp[i][0]=Math.max(dp[i-1][1],dp[i-1][0]);
dp[i][1]=dp[i-1][0]+nums[i-1];
}
return Math.max(dp[n][0],dp[n][1]);
}
}
打家劫舍 II
这道题刚开始没有想出来怎么用dp,所以用dfs,可以做,但是会超时
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
int max=-1;
public int rob(int[] nums) {
//根据第一个房子分两种情况
dfs(nums,1,0,0,0);
dfs(nums,1,1,nums[0],1);
return max;
}
public void dfs(int []nums,int index,int flag,int sum,int start){
if(index==nums.length){
if(sum>max)
max=sum;
return;
}
if(index==nums.length-1&&start==1){
dfs(nums,index+1,0,sum,start);
return;
}
if(flag==1)
dfs(nums,index+1,0,sum,start);
else{
dfs(nums,index+1,0,sum,start);
dfs(nums,index+1,1,sum+nums[index],start);
}
}
}
这道题的区别在于头和尾是不能相邻的,换个思路想那这里就有两种情况:有头就没有尾,有尾就没有头,这两种情况对应了两个范围,那么就可以求这两个范围的最大值,接着进行比较即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public int rob(int[] nums) {
if(nums.length==1)
return nums[0];
else if(nums.length==2)
return Math.max(nums[0],nums[1]);
return Math.max(
robRange(nums,0,nums.length-2),
robRange(nums,1,nums.length-1)
);
}
public int robRange(int[]nums,int start,int end){
int n=end-start+1;
int [][]dp=new int[n+1][2];
dp[0][1]=Integer.MIN_VALUE;
for(int i=1;i<=n;i++){
dp[i][0]=Math.max(dp[i-1][1],dp[i-1][0]);
dp[i][1]=dp[i-1][0]+nums[i+start-1];
}
return Math.max(dp[n][0],dp[n][1]);
}
}
打家劫舍 III (树形DP)
考虑到是二叉树,所以要用递归进行遍历,因为这种是多个分支的结果进行返回的,所以递归函数要带返回值,这种需要考虑这个递归函数返回值是什么,对左右子树的返回值进行处理,然后返回
这里返回值是一个数组,第一位是含有该根节点时最佳值,第二位是不含该根节点的最佳值,所以递归其子树,得到子树对应的值,然后求自己的。数组版是从左到右,这个因为不方便子节点的时候判断父节点,方便父节点的时候判断子节点,所以是反向的
具体步骤如下: 1、构建多阶段决策模型 树形dp基于树这种数据结构上做状态推导,一般都是从下往上推,子节点状态推导父节点状态。一般都是 基于后序遍历来实现。 2、定义状态 每个节点有两个状态:偷,不偷 int money[2]表示每个节点的状态 money[0]:表示选择不偷此节点,当下最大金额 money[1]:表示选择偷此节点,当下的最大金额 3、定义状态转移方程 money[0]=max(leftmoney[0],leftmoney[1]]+max(rightmoney[0],rightmoney[1]) money[1]=leftmoney[0]+rightmoney[0]+root.val
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public int rob(TreeNode root) {
int []res=dfs(root);
return res[0]>res[1]?res[0]:res[1];
}
public int[] dfs(TreeNode node){
if(node==null)
return new int[]{0,0};
int []left=dfs(node.left);
int []right=dfs(node.right);
//v1代表自己要偷,那么子节点就不能偷
//v2代表自己不偷,那么两个子节点就都可以,各自可以偷也可以不偷,求最大值即可
int v1=left[1]+right[1]+node.val;
int v2=Math.max(left[0],left[1])+Math.max(right[0],right[1]);
return new int[]{v1,v2};
}
}
买卖股票的最佳时机
这道题是只能交易一次,也就是说对于持有股票的情况只能是当天购买的股票,就不能叠加前一天没有股票时赚的前
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public int maxProfit(int[] prices) {
int n=prices.length;
int [][]dp=new int[n+1][2];
dp[0][1]=Integer.MIN_VALUE;
for(int i=1;i<=n;i++){
dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+prices[i-1]);
dp[i][1]=Math.max(dp[i-1][1],-prices[i-1]);
}
return Math.max(dp[n][0],dp[n][1]);
}
}
买卖股票的最佳时机 II
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public int maxProfit(int[] prices) {
int n=prices.length;
int [][]dp=new int[n+1][2];
dp[0][1]=Integer.MIN_VALUE;
for(int i=1;i<=n;i++){
dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+prices[i-1]);
dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]-prices[i-1]);
}
return Math.max(dp[n][0],dp[n][1]);
}
}
买卖股票的最佳时机含手续
1、构建多阶段决策模型 n天对应n个阶段,每个阶段决策: 买股票,卖股票,不操作
买股票:只有当前不持有股票才可
卖股票:只有当前持有股票才可
不操作:无限制 2、定义状态 每天有两种状态:持有股票,不持有股票。 int dp[n][2]记录每个阶段的状态 dp[i][0]表示第i天不持有股票,赚到的最大利润 dp[i][1]表示第i天持有股票,赚到的最大利润 3、定义状态转移方程 dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+prices[i]-fee)
dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]-prices[i])
这里不可达设置为Integer.MIN_VALUE/2是因为防止越界,因为后面dp[i-1][1]+prices[i-1]-fee,如果fee很大的话,那就会越界
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public int maxProfit(int[] prices, int fee) {
int n=prices.length;
int [][]dp=new int[n+1][2];
dp[0][1]=Integer.MIN_VALUE/2;
for(int i=1;i<=n;i++){
dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]-prices[i-1]);
dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+prices[i-1]-fee);
}
return Math.max(dp[n][0],dp[n][1]);
}
}
最佳买卖股票时机含冷冻期
这道题相对于上道题来说,区别在于多了一个冷冻期,即前一天卖了股票,今天是不能买股票的
就相当于有三种状态:
- 今天有股票,可能是昨天就有的,或者今天买的
- 今天没有股票且处于冷冻期,那么只有可能是今天卖了股票
- 今天没有股票且没有处于冷冻期,那么就有可能是前一天是冷冻期或者前一天非冷冻期但也没有股票
这里说的第i天处于冷冻期,指的是第i天卖了股票,第i+1天不能买股票
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public int maxProfit(int[] prices) {
int n=prices.length;
int [][]dp=new int[n+1][3];
dp[0][1]=Integer.MIN_VALUE;
for(int i=1;i<=n;i++){
dp[i][0]=Math.max(dp[i-1][0],dp[i-1][2]);
dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]-prices[i-1]);
dp[i][2]=dp[i-1][1]+prices[i-1];
}
return Math.max(Math.max(dp[n][0],dp[n][1]),dp[n][2]);
}
}
买卖股票的最佳时机 III
之前是先初始化第0天的阶段,接着处理后面的天数,但这样的前提是prices不为空,所以为了避免这种情况出现,就初始化第-1天,后面每天进行判断
初始化-1天的话,有一些状态就是不可达的,主要有两个:
第一个是第-1天是不能持有股票的,所以是不可达的
第二个是购买的状态也不能是负数,也是不可达的
所以对应数组的时候,因为数组不能为负,所以所有状态后面移动一位,至于状态方程和之前的类似,区别在于要加一个for循环,来对所有状态的j进行求最佳值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public int maxProfit(int[] prices) {
int[][][]dp=new int[prices.length+1][4][2];
for(int i=0;i<=prices.length;i++)
for(int j=0;j<2;j++)
dp[i][0][j]=Integer.MIN_VALUE;
for(int i=0;i<=3;i++)
dp[0][i][1]=Integer.MIN_VALUE;
for(int i=1;i<=prices.length;i++){
for(int j=1;j<=3;j++){
dp[i][j][0]=Math.max(dp[i-1][j][0],dp[i-1][j-1][1]+prices[i-1]);
dp[i][j][1]=Math.max(dp[i-1][j][1],dp[i-1][j][0]-prices[i-1]);
}
}
return dp[prices.length][3][0];
}
}
买卖股票的最佳时机 IV
和上题一样,区别在于将2改成k
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public int maxProfit(int k, int[] prices) {
int[][][]dp=new int[prices.length+1][k+2][2];
for(int i=0;i<=prices.length;i++)
for(int j=0;j<2;j++)
dp[i][0][j]=Integer.MIN_VALUE;
for(int i=0;i<=k+1;i++)
dp[0][i][1]=Integer.MIN_VALUE;
for(int i=1;i<=prices.length;i++){
for(int j=1;j<=k+1;j++){
dp[i][j][0]=Math.max(dp[i-1][j][0],dp[i-1][j-1][1]+prices[i-1]);
dp[i][j][1]=Math.max(dp[i-1][j][1],dp[i-1][j][0]-prices[i-1]);
}
}
return dp[prices.length][k+1][0];
}
}
爬楼梯问题
都是一条完整的串,可以由几个子串拼接而成,对于这种问题,可以考虑爬楼梯的解法
每一步可以走X,Y,Z个台阶,走完n个台阶,问:
- 有多少种走法
- 至少需要多少步
- 能否刚好走完
多阶段决策模型:
阶段个数不固定,每个阶段决策走多少个台阶
状态定义:
- int dp[n+1] dp[i]表示走完i个台阶有多少个走法
- int dp[n+1] dp[i]表示走完i个台阶有至少需要多少步
- boolean dp[n+1] dp[n]表示是否刚好走完i个台阶
状态转移方程:
到达i个状态,那一步只能是走x,y,z个台阶,也就是从i-x,i-y,i-z转化过来,即由dp[i-x],dp[i-y],dp[i-z]转化推导出来
- dp[i]=dp[i-x]+dp[i-y]+dp[i-z]
- dp[i]=Math.min(Math.min(dp[i-x],dp[i-y]),dp[i-z])+1
-
dp[i]=dp[i-x] dp[i-y] dp[i-z]
爬楼梯
dp[i]只有从dp[i-1]、dp[i-2]前两个状态转移过来
1
2
3
4
5
6
7
8
9
class Solution {
public int climbStairs(int n) {
int []dp=new int[n+1];
dp[0]=1;dp[1]=1;
for(int i=2;i<=n;i++)
dp[i]=dp[i-1]+dp[i-2];
return dp[n];
}
}
零钱兑换
也可以作为爬楼梯问题,比如现在硬币是1,2,5,amount是11,可以理解为阶梯是11,现在可以走1步,2步5步,最少需要多少步,所以只需要考虑对于当前i,所有可以达到他的状态的最小值即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public int coinChange(int[] coins, int amount) {
int k=coins.length;
int []dp=new int[amount+1];
Arrays.fill(dp,amount+1);
dp[0]=0;
for(int i=1;i<=amount;i++){
//这一重循环是有k种方式可以到当前阶段
for(int j=0;j<k;j++){
if(i-coins[j]>=0)
dp[i]=Math.min(dp[i],dp[i-coins[j]]+1);
}
}
return dp[amount]==amount+1?-1:dp[amount];
}
}
下面这种是以背包问题进行考虑,可以分析一下两者的区别
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public int coinChange(int[] coins, int amount) {
int [][]dp=new int[coins.length+1][amount+1];
for(int []d:dp)
Arrays.fill(d,Integer.MAX_VALUE/2);
dp[0][0]=0;
for(int i=1;i<=coins.length;i++){
for(int j=0;j<=amount;j++){
if(j<coins[i-1]){
dp[i][j]=dp[i-1][j];
}else{
dp[i][j]=Math.min(dp[i-1][j],dp[i][j-coins[i-1]]+1);
}
}
}
return dp[coins.length][amount]==Integer.MAX_VALUE/2?-1:dp[coins.length][amount];
}
}
零钱兑换 II
那对于求个数是否可以用爬楼梯问题解决呢?实际上是不行的,对于这道题,是求组合的个数,它是不考虑顺序的,1+5+5和5+1+5对于这道题来说这是一种解法,而对于爬楼梯的思路来说是两种解法,所以是不对的,所以这道题要用背包的思想,就是完全背包的计数问题,背包问题就计数的时候都是考虑哪个硬币多少个,是没有考虑顺序的
换句话来说背包问题是求解不考虑顺序的计数,爬楼梯是求讲顺序的计数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public int change(int amount, int[] coins) {
int[][]dp=new int[coins.length+1][amount+1];
dp[0][0]=1;
for(int i=1;i<=coins.length;i++){
for(int j=0;j<=amount;j++){
if(j<coins[i-1]){
dp[i][j]=dp[i-1][j];
}else{
dp[i][j]=dp[i-1][j]+dp[i][j-coins[i-1]];
}
}
}
return dp[coins.length][amount];
}
}
下面这用爬楼梯思路来做,但不适用于这道题
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public int change(int amount, int[] coins) {
int[]dp=new int[amount+1];
dp[0]=1;
for(int i=1;i<=amount;i++){
for(int j=0;j<coins.length;j++){
if(i-coins[j]>=0)
dp[i]+=dp[i-coins[j]];
}
}
dp[amount];
}
}
砍竹子 I
这里用爬楼梯的思路,对于dp[i]来说,其可以由dp[i-1],dp[i-2],…dp[0]转移过来,只是区别在于之间的跨步,所以可以由状态转移方程推导dp[i] = Math.max(dp[i], j * dp[i - j]);
因为题意是需要切割的,对于n<=3的情况,其实不切割的长度更长,属于是特殊情况,单独列出即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public int cuttingBamboo(int bamboo_len) {
if(bamboo_len==3)
return 2;
int[] dp = new int[bamboo_len + 1];
dp[0]=1;
for (int i = 1; i <= bamboo_len; i++) {
for (int j = 1; j <=i; j++) {
dp[i] = Math.max(dp[i], j * dp[i - j]);
}
}
return dp[bamboo_len];
}
}
解密数字
这道题用dfs也能做
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
int count=0;
public int crackNumber(int ciphertext) {
dfs(Integer.toString(ciphertext),0);
return count;
}
public void dfs(String ciphertext,int index){
if(index==ciphertext.length()){
count++;
return;
}
for(int i=0;i<2&&index+i<ciphertext.length();i++){
if(i==0){
dfs(ciphertext,index+1);
}else if(ciphertext.charAt(index)=='1'
||(ciphertext.charAt(index)=='2'&&ciphertext.charAt(index+1)<'6')){
dfs(ciphertext,index+2);
}
}
}
}
用动态规划的话,就是将上面dfs的思路转化成状态方程,如果能凑成两位数在10-25之间,就可以加上dp[i-2],否则只能加上dp[i-1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public int crackNumber(int ciphertext) {
String text=Integer.toString(ciphertext);
int len=text.length();
int []dp=new int[len+1];
dp[0]=1;dp[1]=1;
for(int i=2;i<=len;i++){
if(text.charAt(i-2)=='1'
||(text.charAt(i-2)=='2'&&text.charAt(i-1)<'6'))
dp[i]=dp[i-1]+dp[i-2];
else
dp[i]=dp[i-1];
}
return dp[len];
}
}
单词拆分
也可以使用dfs来做,代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
int []visited;
HashSet<String>Dict;
public boolean wordBreak(String s, List<String> wordDict) {
int n=s.length();
visited=new int[n];
Arrays.fill(visited,-1);
Dict=new HashSet<>(wordDict);
return dp(s,0);
}
public boolean dp(String s,int i){
if(i==s.length())
return true;
if(visited[i]!=-1){
return false;
}
visited[i]=0;
for(int len=1;len+i<=s.length();len++){
String prix=s.substring(i,i+len);
if(Dict.contains(prix)){
boolean flag=dp(s,i+len);
if(flag==true){
return true;
}
}
}
return false;
}
}
和上题思路一样,不过这道题的匹配字符串长度不一样,所以需要设置一个起始位true的点,接着遍历list里的每个word,设置可达点
对于每个位置是否为true,取决于这个位置是否由其他字典拼接能够到达
| 在字符串匹配的情况下 dp[i]=dp[i-len1] | dp[i-len2] | dp[i-len3] |
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
boolean []dp=new boolean[s.length()+1];
dp[0]=true;
for(int i=0;i<=s.length();i++){
if(dp[i]==true){
for(String word:wordDict){
if(i+word.length()<=s.length()&&s.substring(i,i+word.length()).equals(word))
dp[i+word.length()]=true;
}
}
}
return dp[s.length()];
}
}
交错字符串
对于字符串s3来说,如果第i+j个位置是与s1的i相等的,那么只要dp[i-1][j]是可达的,则dp[i][j]就是可达的,同理s2也是一样的,所以这道题的状态方程就是
| dp[i][j]=( dp[i-1][j]&&s1.charAt(i-1)==s3.charAt(i+j-1) | dp[i][j-1]&&s2.charAt(j-1)==s3.charAt(i+j-1) ); |
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public boolean isInterleave(String s1, String s2, String s3) {
int n=s1.length();
int m=s2.length();
int t=s3.length();
if(n+m!=t)
return false;
boolean[][]dp=new boolean[n+1][m+1];
dp[0][0]=true;
for(int i=1;i<=n;i++)
dp[i][0]=dp[i-1][0]&&s1.charAt(i-1)==s3.charAt(i-1);
for(int j=1;j<=m;j++)
dp[0][j]=dp[0][j-1]&&s2.charAt(j-1)==s3.charAt(j-1);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
dp[i][j]=(dp[i-1][j]&&s1.charAt(i-1)==s3.charAt(i+j-1)
||dp[i][j-1]&&s2.charAt(j-1)==s3.charAt(i+j-1));
}
}
return dp[n][m];
}
}
匹配问题
这类问题分为两个步骤
- 对0行和0列初始化
- 双重for填写其他的位置
编辑距离
这类题都这个思路,画下这个表,接着进行判断
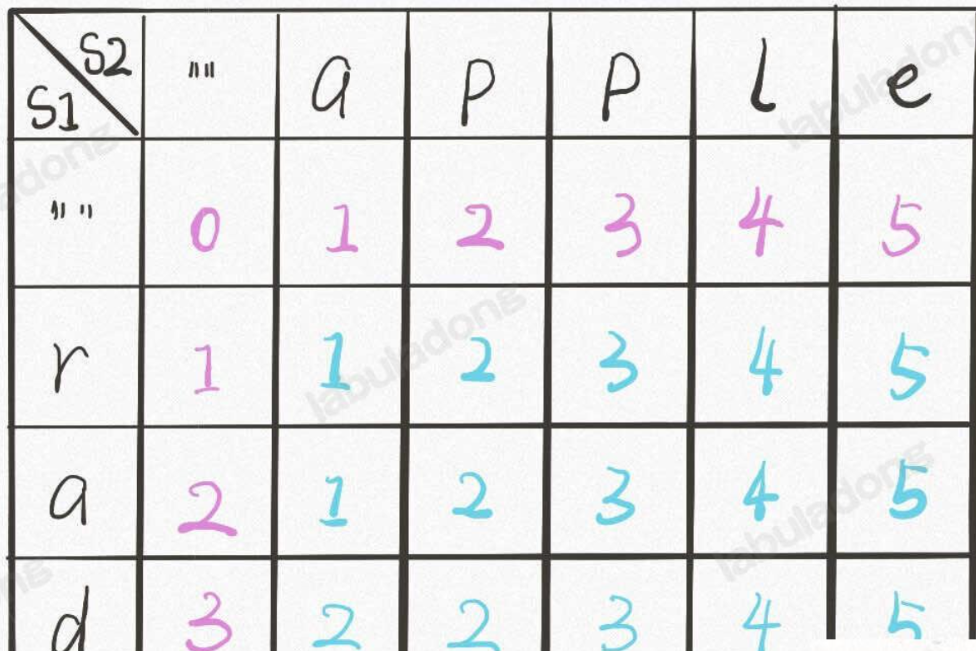
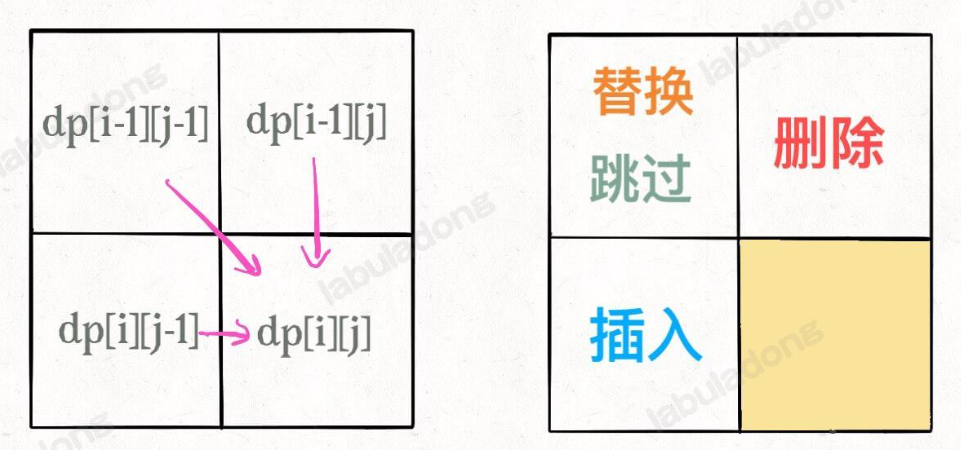
编辑距离相当于是将一个字符串变为另一个字符串的过程,那也就是说一个字符串不变,对另一个字符串进行操作(增、删、替换),来变成和另一个字符串相同
从dp[i-1][j]->dp[i][j]就可以理解为s2删除了当前不相同的字符,前进了一步到当前阶段
dp[i][j-1]->dp[i][j]可以理解为s2插入了一个元素,它当前的指针是不变的,s1已经有匹配到的了,所以j前进一步
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public int minDistance(String word1, String word2) {
int m=word1.length();
int n=word2.length();
int [][]dp=new int[m+1][n+1];
for(int i=0;i<=n;i++)
dp[0][i]=i;
for(int j=0;j<=m;j++)
dp[j][0]=j;
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
if(word1.charAt(i-1)==word2.charAt(j-1)){
dp[i][j]=dp[i-1][j-1];
}else{
dp[i][j]=Math.min(
dp[i-1][j],
Math.min(dp[i-1][j-1],dp[i][j-1])
)+1;
}
}
}
return dp[m][n];
}
}
最长公共子序列
还是考虑当前状态dp[i][j]可以由哪些状态转移过来
如果t1[i-1]等于t2[j-1]的话,那就可以是由(i-1,j)、(i,j-1)、(i-1,j-1)转移过来
如果t1[i-1]不等于t2[j-1]的话,那就可以是由(i-1,j)、(i,j-1)转移过来
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int m=text1.length();
int n=text2.length();
int [][]dp=new int[m+1][n+1];
for(int i=0;i<=m;i++)
dp[i][0]=0;
for(int i=0;i<=n;i++)
dp[0][i]=0;
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
if(text1.charAt(i-1)==text2.charAt(j-1))
dp[i][j]=Math.max(Math.max(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1]+1);
else
dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
}
}
return dp[m][n];
}
}
两个字符串的删除操作
思路一样的,对于这种两个字符串进行操作匹配的,都可以利用这种方式求解,先画一个dp表,然后根据其中的规律写状态方程,然后代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public int minDistance(String word1, String word2) {
int m=word1.length();
int n=word2.length();
int [][]dp=new int[m+1][n+1];
for(int i=0;i<=m;i++)
dp[i][0]=i;
for(int j=0;j<=n;j++)
dp[0][j]=j;
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
if(word1.charAt(i-1)==word2.charAt(j-1))
dp[i][j]=dp[i-1][j-1];
else{
dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+1;
}
}
}
return dp[m][n];
}
}
两个字符串的最小ASCII删除和
这道题的区别是使用ascii码,我最开始算错了,是因为在最开始设置数组的第一行和第一列的时候,是直接设置的s1.charAt(i-1),这应该是叠加的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public int minimumDeleteSum(String s1, String s2) {
int m=s1.length();
int n=s2.length();
int [][]dp=new int[m+1][n+1];
for(int i=1;i<=m;i++)
dp[i][0]=s1.charAt(i-1)+dp[i-1][0];
for(int i=1;i<=n;i++)
dp[0][i]=s2.charAt(i-1)+dp[0][i-1];
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
if(s1.charAt(i-1)==s2.charAt(j-1)){
dp[i][j]=dp[i-1][j-1];
}else{
dp[i][j]=Math.min(
dp[i-1][j]+s1.charAt(i-1),
dp[i][j-1]+s2.charAt(j-1)
);
}
}
}
return dp[m][n];
}
}
求矩阵正方形
最大正方形
这个题是求矩阵最大正方形的面积,也就是求最大正方形的边长
所以这类题的状态dp[i][j]表示以(i,j)为右下角的正方形的最长边长
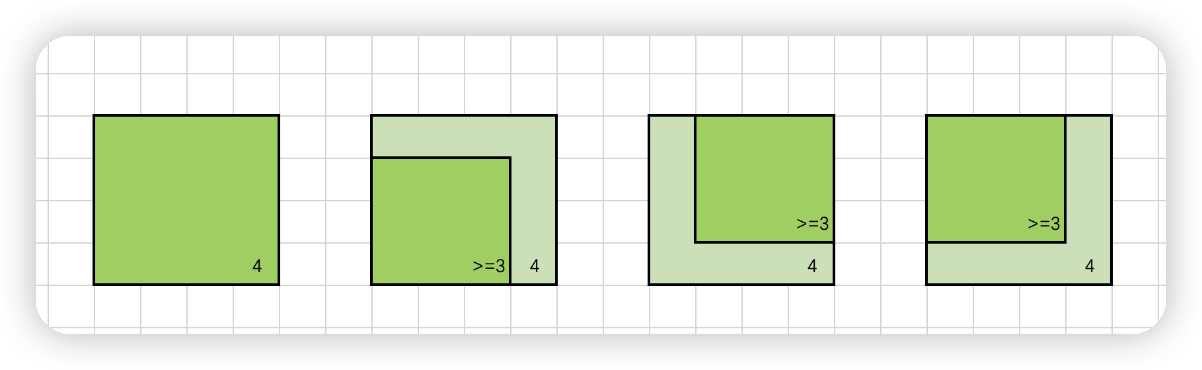
从上面这个图可以看出来,对于一个以(i,j)为右下角的正方形来说,他的边长由(i-1,j)(i-1,j-1)(i,j-1)这三个位置的最小值决定,这三个值的最小值才能决定(i,j)的边长
所以状态方程是:dp[i][j]=Math.min(dp[i-1][j], Math.min(dp[i-1][j-1], dp[i][j-1])) + 1;
实际上上面这个状态方程只是用于求以(i,j)为右下角的最大正方形,需要用一个maxLength来实时记录整个矩形的最大边长
这里需要考虑边界问题,对于在第0行和第0列的点来说,如果matrix[i][j]=’1’,那dp[i][j]只能是1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public int maximalSquare(char[][] matrix) {
int maxLength=-1;
if(matrix==null||matrix.length==0||matrix[0].length==0)
return 0;
int m=matrix.length;int n=matrix[0].length;
int [][]dp=new int[m][n];
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(matrix[i][j]=='1'){
if(i==0||j==0){
dp[i][j]=1;
}else{
dp[i][j]=Math.min(dp[i-1][j],
Math.min(dp[i-1][j-1],dp[i][j-1]))+1;
}
maxLength=Math.max(maxLength,dp[i][j]);
}
}
}
return maxLength==-1?0:maxLength*maxLength;
}
}
统计全为 1 的正方形子矩阵
基本和上题一样,区别在于是求正方形个数,这里有一个点在于对于一个以(i,j)为右下角的正方形来说,它能增加的正方形数量取决于它的边长,dp[i][j] = x 也表示以 (i, j) 为右下角的正方形的数目为 x(即边长为 1, 2, …, x 的正方形各一个)
所以核心思路还是求每个以(i,j)为右下角的正方形的最大边长,找到每个位置的边长,就能找到每个位置多出来的正方形数量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public int countSquares(int[][] matrix) {
if(matrix==null||matrix.length==0||matrix[0].length==0)
return 0;
int count=0;
int m=matrix.length;int n=matrix[0].length;
int [][]dp=new int[m][n];
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(matrix[i][j]==1){
if(i==0||j==0){
dp[i][j]=1;
}else{
dp[i][j]=Math.min(dp[i-1][j],
Math.min(dp[i-1][j-1],dp[i][j-1]))+1;
}
}
count+=dp[i][j];
}
}
return count;
}
}
其他
最长递增子序列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public int lengthOfLIS(int[] nums) {
int[]dp=new int[nums.length];
Arrays.fill(dp,1);
int max=1;
for(int i=1;i<nums.length;i++){
for(int j=0;j<i;j++){
if(nums[i]>nums[j])
dp[i]=Math.max(dp[i],dp[j]+1);
}
max=Math.max(max,dp[i]);
}
return max;
}
}
路径总和III(树形DP)
这道题可以用bfs+dfs来做,bfs遍历树的每个节点,接着用dfs遍历每个节点看是否sum满足Target
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
int count=0;
public int pathSum(TreeNode root, int targetSum) {
if(root==null)
return 0;
Queue<TreeNode>queue=new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
int size=queue.size();
for(int i=0;i<size;i++){
TreeNode node=queue.poll();
NodeSum(node,targetSum,0);
if(node.left!=null)queue.add(node.left);
if(node.right!=null)queue.add(node.right);
}
}
return count;
}
public void NodeSum(TreeNode node,int Target,long sum){
if(node==null)
return;
sum+=node.val;
if(sum==Target)
count++;
NodeSum(node.left,Target,sum);
NodeSum(node.right,Target,sum);
}
}
树形dp
思路还是和之前那道树形dp那道思路相似,还是要dfs,在dfs的过程中,遍历子节点的时候需要返回当前阶段需要的状态值,当前节点在对此进行dp,再返回
当前节点的Map<Long,Integer>代表子节点的路径和当前节点求和之后的新的sum的条数,key是新的sum,value是这个sum对应的条数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
int count=0;
public int pathSum(TreeNode root, int targetSum) {
dfs(root,targetSum);
return count;
}
public Map<Long,Integer> dfs(TreeNode node,long targetSum){
if(node==null)return new HashMap<>();
Map<Long,Integer>left=dfs(node.left,targetSum);
Map<Long,Integer>right=dfs(node.right,targetSum);
Map<Long,Integer>rootValue=new HashMap<>();
long val=node.val;
rootValue.put(val,1);
for(Map.Entry<Long,Integer>entry:left.entrySet()){
rootValue.put(val+entry.getKey(),rootValue.getOrDefault(val+entry.getKey(),0)+entry.getValue());
}
for(Map.Entry<Long,Integer>entry:right.entrySet()){
rootValue.put(val+entry.getKey(),rootValue.getOrDefault(val+entry.getKey(),0)+entry.getValue());
}
if(rootValue.containsKey(targetSum))
count+=rootValue.get(targetSum);
return rootValue;
}
}
找出有效子序列的最大长度 I
这道题其实也不算dp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public int maximumLength(int[] nums) {
int ji=0,ou=0,hun=1;
if(nums[0]%2==1)
ji++;
else
ou++;
for(int i=1;i<nums.length;i++){
if(nums[i]%2==0)
ou++;
else
ji++;
if(nums[i-1]%2!=nums[i]%2)
hun++;
}
return Math.max(ji,Math.max(ou,hun));
}
}
找出有效子序列的最大长度 II
dp[n][k]表示对于第n个数,相邻为k的最长长度,这个属于暴力dp,也属于是经典找子序列的方式,上题也可以用,不过会超时。
主要思路就是把里面这层for循环都作为子序列候选人,当前nums[i]会和其前面i个数都求和求余,然后更新对对应的长度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public int maximumLength(int[] nums, int k) {
int res=-1;
int n=nums.length;
int [][]dp=new int[n][k];
for(int []d:dp)
Arrays.fill(d,1);
for(int i=1;i<n;i++){
for(int j=0;j<i;j++){
dp[i][(nums[i]+nums[j])%k]=dp[j][(nums[i]+nums[j])%k]+1;
res=Math.max(res,dp[i][(nums[i]+nums[j])%k]);
}
}
return res;
}
}
对于这道题,还有一个更简单的方式,首先有个前置知识,题目要求(a+b)modk=(b+c)modk,通过对这个式子的变形,可以得到(a−c)modk=0,即a和c同模即可,而c=a+1,所以翻译过来就是有效子序列的奇数项都关于模 k 同余,偶数项都关于模 k 同余
原问题等价于:寻找一个最长的子序列,满足子序列奇数项都相同,偶数项都相同
要保证上面这个条件,说明这个序列取模之后只有两个数(这两个数也可以相等),奇数项是一个数,偶数项是一个数,也就是说只要知道序列的后两位,就可以找到整个子序列。
所以定义dp[x][y],表示在目前子序列中,x是倒数第二个模,y是最后一个模,以这两个模为子序列的长度最长,那当遍历到一个数,其模为n,此时他为序列的最后一位,那么只需要遍历模为0-k-1的y找其中dp[n][y]最长的一个即可,所以状态方程为:dp[y][n]=dp[n][y]+1,这个表示目前以n为最后一个模的子序列长度等于以y为最后一个模的子序列长度加1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public int maximumLength(int[] nums, int k) {
int res=-1;
int [][]dp=new int[k][k];
for(int n:nums){
n=n%k;
for(int y=0;y<k;y++){
dp[y][n]=dp[n][y]+1;
res=Math.max(res,dp[y][n]);
}
}
return res;
}
}