数据结构学习
数据结构:线性结构+非线形结构
线性结构

非线形结构
数组、广义表、树、图
稀疏数组

处理方式

实例
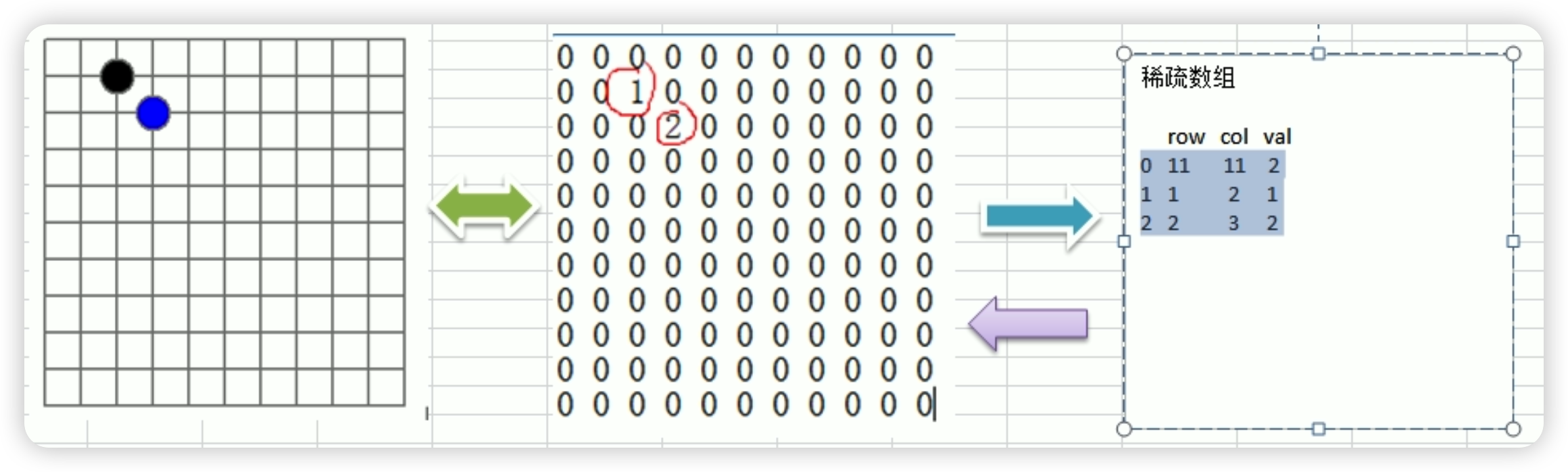
稀疏矩阵与二维数组转化思路

代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
package sparseArray;
import java.io.*;
import java.util.ArrayList;
import java.util.Stack;
import java.io.IOException;
public class sparseArray {
public static void main(String[] args) {
int array[][] = new int[11][11];
array[1][2] = 1;
array[4][5] = 3;
//输出数组
for (int row[] : array) {
for (int data : row) {
System.out.printf("%d\t", data);
}
System.out.println();
}
//array to sparse
int res[][]=arraytosparse(array);
for (int row[] : res) {
for (int data : row) {
System.out.printf("%d\t", data);
}
System.out.println();
}
//sparse to array
int res2[][]=sparsetoarray(res);
for (int row[] : res2) {
for (int data : row) {
System.out.printf("%d\t", data);
}
System.out.println();
}
//io
save(res2);
int res3[][]=read();
for (int row[] : res2) {
for (int data : row) {
System.out.printf("%d\t", data);
}
System.out.println();
}
}
public static int[][] arraytosparse(int [][]array){
int num=0;
Stack<Integer>stack=new Stack<>();
for(int i=0;i<array.length;i++){
for(int j=0;j<array[0].length;j++){
if(array[i][j]!=0){
num++;
stack.push(i);
stack.push(j);
stack.push(array[i][j]);
}
}
}
int res[][]=new int[num+1][3];
res[0][0]=array.length;
res[0][1]=array[0].length;
res[0][2]=num;
int i=1;
while (!stack.isEmpty()){
res[i][2]=stack.pop();
res[i][1]=stack.pop();
res[i][0]=stack.pop();
i++;
}
return res;
}
public static int[][] sparsetoarray(int sparse[][]){
int res[][]=new int[sparse[0][0]][sparse[0][1]];
for(int k=1;k<sparse.length;k++){
res[sparse[k][0]][sparse[k][1]]=sparse[k][2];
}
return res;
}
public static void save(int array[][]){
try {
FileOutputStream fileOutputStream=new FileOutputStream("map.data");
ObjectOutputStream objectOutputStream=new ObjectOutputStream(fileOutputStream);
objectOutputStream.writeObject(array);
objectOutputStream.close();
fileOutputStream.close();
System.out.println("已保存");
}catch (IOException ioe){
ioe.printStackTrace();
}
}
public static int[][] read() {
try {
FileInputStream fileInputStream=new FileInputStream("map.data");
ObjectInputStream objectInputStream=new ObjectInputStream(fileInputStream);
int array[][]= (int[][]) objectInputStream.readObject();
objectInputStream.close();
fileInputStream.close();
return array;
}catch (FileNotFoundException e) {
throw new RuntimeException(e);
} catch (IOException e) {
throw new RuntimeException(e);
} catch (ClassNotFoundException e) {
throw new RuntimeException(e);
}
}
}
队列
单向队列
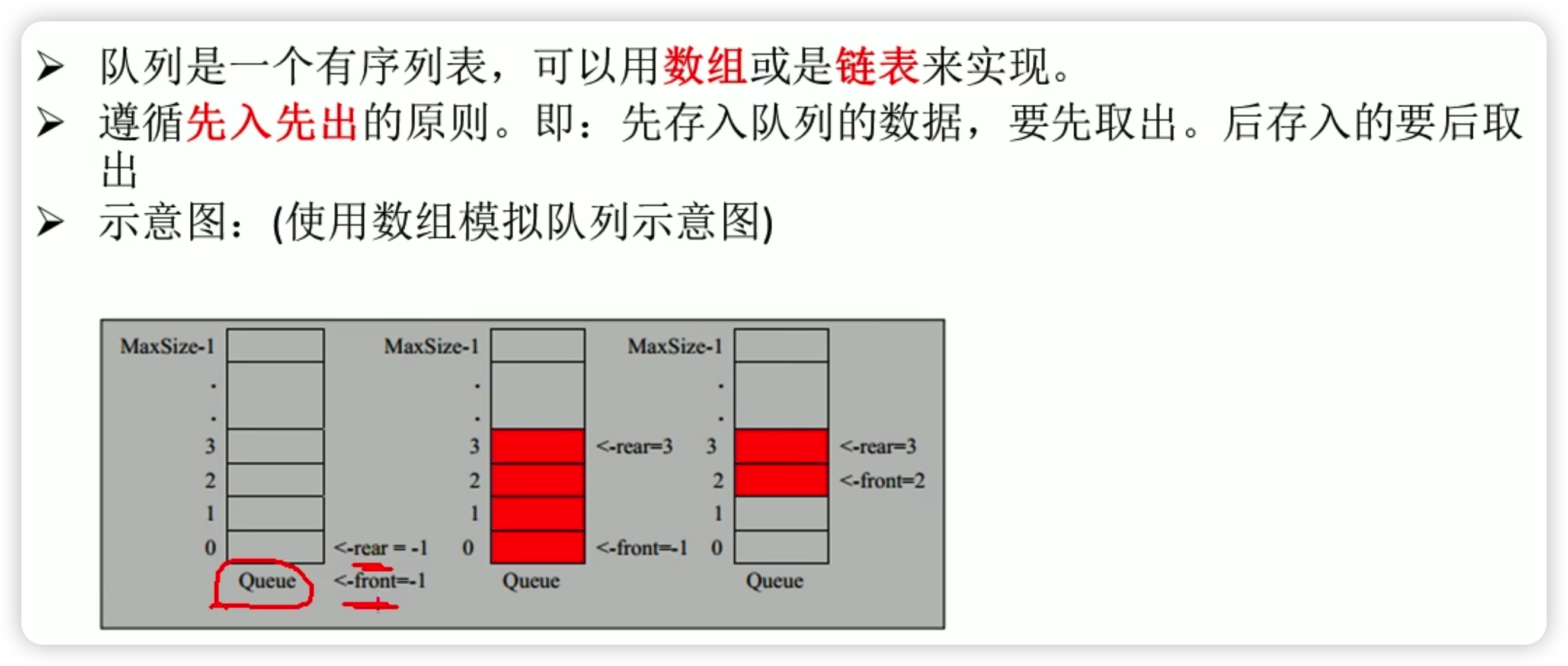
数组模拟队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
class ArrayQueue{
private int MaxSize; //队列最大容积
private int front; //队列头 代表当前位置的下一个有数据
private int rear; //队列尾 代表当前位置为最后一个数据
private int[] arr; //模拟队列
public void ArrayQueue(int arrayMaxSize){
MaxSize=arrayMaxSize;
arr=new int[MaxSize];
front=-1;
rear=-1;
}
//判断队列是否满
public boolean isFull(){
return rear==MaxSize-1;
}
//判断队列是否为空
public boolean isempty(){
return front==rear;
}
//进队列
public void addQueue(int data){
if(isFull()){
System.out.println("队列已满");
return;
}
arr[++rear]=data;
System.out.println("添加成功");
return;
}
//出队列
public int getQueue(){
if(isempty()){
throw new RuntimeException("队列空");
}
int res=arr[++front];
return res;
}
//输出队列
public void showQueue(){
if(isempty()){
System.out.println("队列为空");
return;
}
for(int i=front+1;i<=rear;i++){
System.out.printf("%d\t",arr[i]);
}
return;
}
}
环形队列

和单独队列的front和rear的意义不一样,rear指向的是最后一个位置的下一个,这样的话就需要预留一个空间,否则就会和front相撞
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class CircleArrayQueue{
private int MaxSize; //队列最大容积
private int front; //队列头 代表第一个数据
private int rear; //队列尾 代表当前位置为最后一个数据的下一个
private int[] arr; //模拟队列
public CircleArrayQueue(int maxSize){
MaxSize=maxSize;
front=0;
rear=0;
arr=new int[MaxSize];
}
public boolean isFull(){
return (rear+1)%MaxSize==front;
}
public boolean isEmpty(){
return rear==front;
}
public void addQueue(int data){
if(isFull()){
throw new RuntimeException("队列已满");
}
arr[rear++]=data;
rear=rear%MaxSize;
return;
}
public int getQueue(){
if(isEmpty()){
throw new RuntimeException("队列为空");
}
int res=arr[front++];
front=front%MaxSize;
return res;
}
public void showQueue(){
if(isEmpty()){
System.out.println("队列为空");
return ;
}
//计算有效数据的数量
int count=(rear-front+MaxSize)%MaxSize;
for(int i=front;i<(rear+count);i++){
System.out.printf("%d\t",arr[i%MaxSize]);
}
}
}
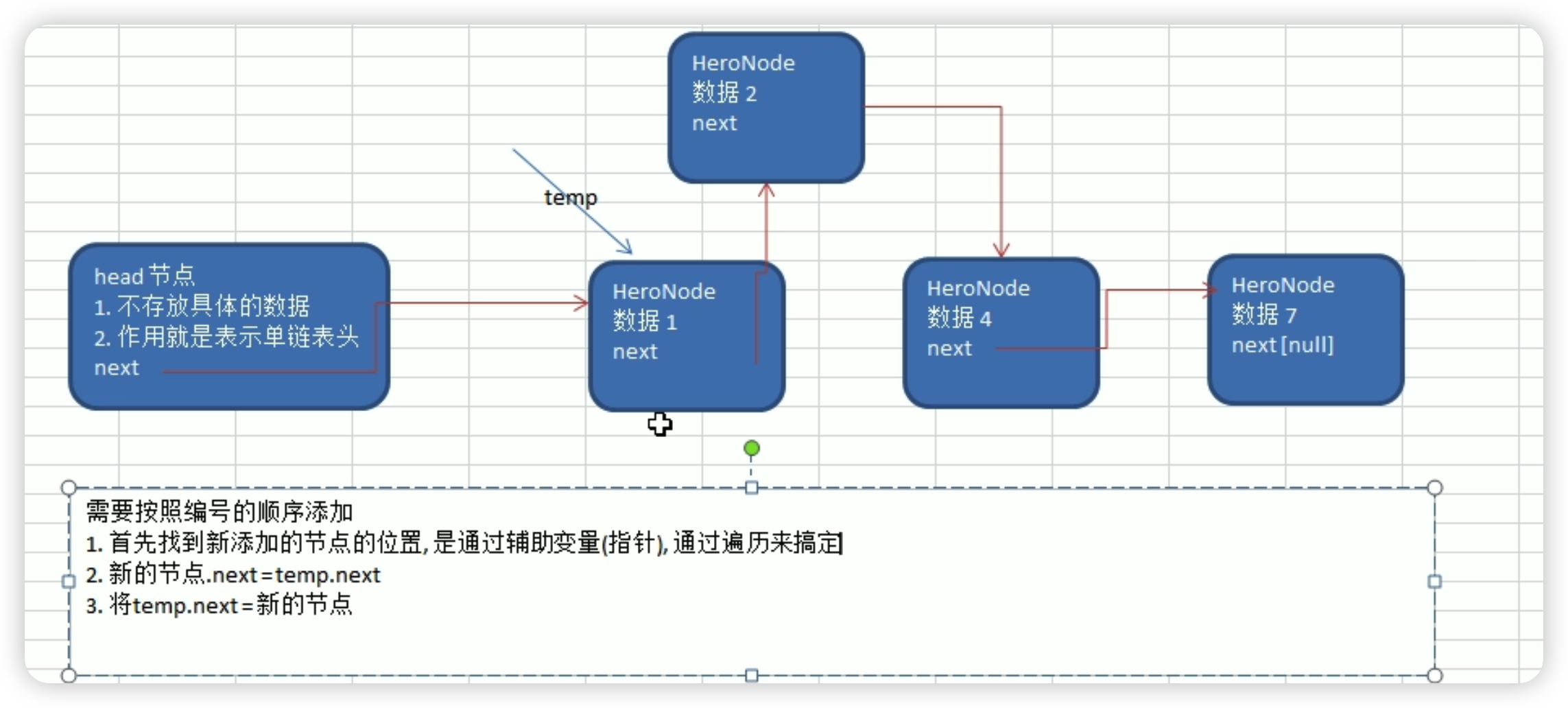
链表
单向链表
插入中间节点
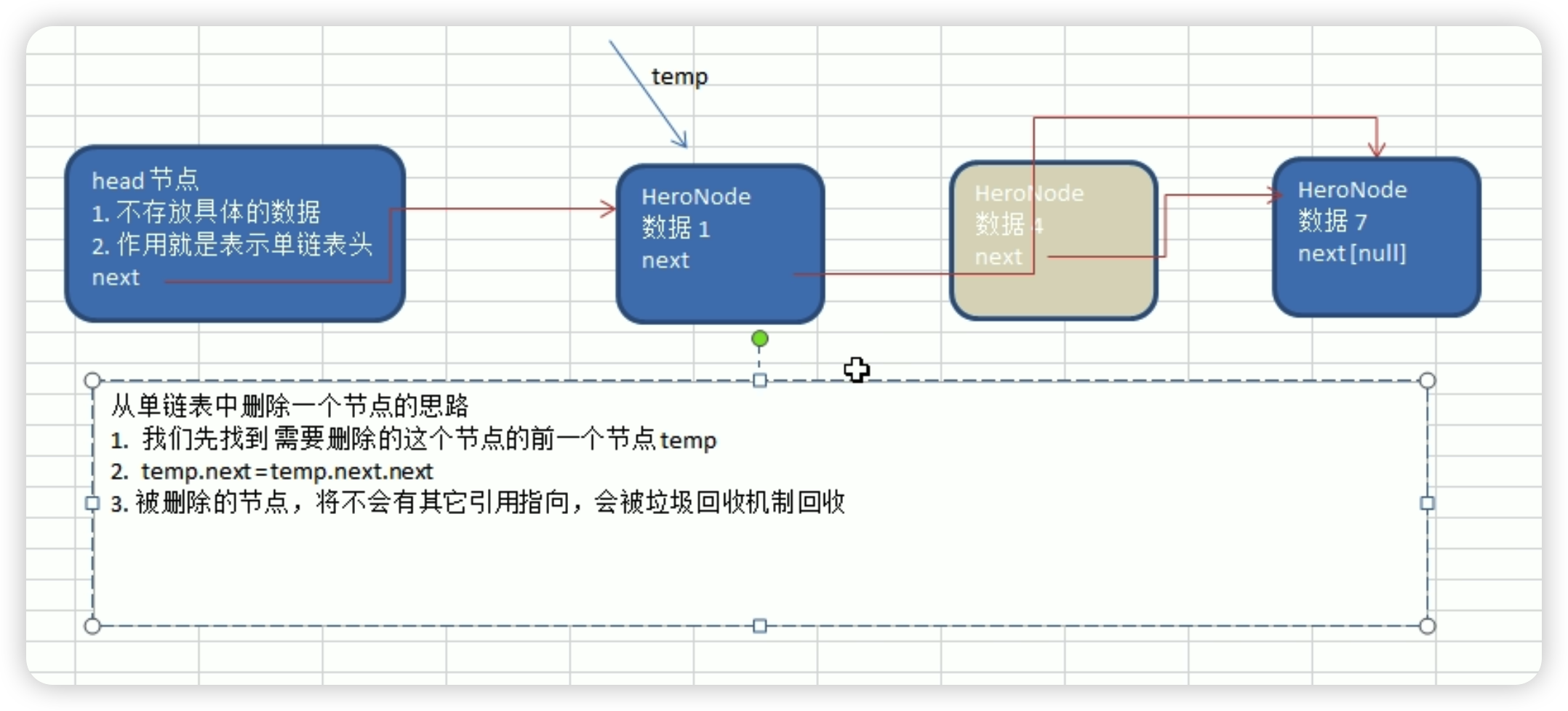
删除节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
package linkedlist;
//定义一个链表
class Listnode {
public int no;
public String name;
public Listnode next;
public Listnode(int lno, String lname) {
this.name = lname;
this.no = lno;
}
@Override
public String toString() {
return "listnode{" +
"no=" + no +
", name='" + name + '\'' +
'}';
}
}
public class SingleLinkedList {
public Listnode head = new Listnode(0, "");
public static void main(String[] args) {
Listnode a = new Listnode(1, "1");
Listnode b = new Listnode(2, "2");
Listnode c = new Listnode(3, "3");
Listnode d = new Listnode(4, "4");
Listnode e = new Listnode(5, "5");
SingleLinkedList singleLinkedList = new SingleLinkedList();
singleLinkedList.addlist(a);
singleLinkedList.addlist(b);
singleLinkedList.addlist(c);
singleLinkedList.addlist(d);
singleLinkedList.show();
singleLinkedList.insert(e, 2);
singleLinkedList.show();
singleLinkedList.delete(5);
singleLinkedList.show();
}
//从链表最后位置添加链表
public void addlist(Listnode listnode) {
Listnode temp = head;
while (temp.next != null) {
temp = temp.next;
}
temp.next = listnode;
}
//显示链表
public void show() {
if (head.next == null) {
System.out.println("空");
return;
}
Listnode listnode = head.next;
while (listnode != null) {
System.out.println(listnode.name);
listnode = listnode.next;
}
return;
}
//从中间插入链表
public void insert(Listnode listnode, int no) {
if (head.next == null) {
System.out.println("链表为空");
return;
}
Listnode temp = head.next;
while (temp != null) {
if (temp.no == no) {
//主要是下面这两步,先把后面的位置给listnode,再让temp指向listnode
listnode.next = temp.next;
temp.next = listnode;
return;
}
temp = temp.next;
}
System.out.println("未找到该节点");
return;
}
//删除节点注意的是temp从head开始,这样就可以while的时候用temp.next,因为一直需要判断的是temp.next
public void delete(int no) {
if (head.next == null)
return;
Listnode temp = head;
while (temp.next != null) {
if (temp.next.no == no) {
temp.next = temp.next.next;
return;
}
temp = temp.next;
}
System.out.println("未找到");
return;
}
}
一般都是head节点不动,然后用temp节点来动,就取决于是temp=head还是temp=head.next,像插入节点这种,直接和节点相关的,就可以temp=head.next,如果是像删除或者创造链表这种和next相关的就可以temp=head
单链表题目
-
求单链表有效节点个数
1 2 3 4 5 6 7 8 9 10 11 12
public void q1(Linkedlist head){ if(head.next==null){ System.out.println("null"); return; } Linkedlist temp=head.next; while(temp!=null){ System.out.printf("%d\t", temp.no); temp=temp.next; } }
-
查找单链表的倒数第k个节点
设置两个链表,让第一个链表先跑k个节点,再让第二个链表跑,第一个链表跑到最后时,第二个链表就为倒数第k个,需要注意的是第一个链表跑的时候需要一直判断是否为空,即判断链表长度是否有k个
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
public void q2(Linkedlist head,int no){ if(head.next==null){ System.out.println("链表为空"); return; } Linkedlist l1=head; for(int i=0;i<no;i++){ l1=l1.next; if(l1==null){ System.out.printf("链表数量不够%d个",no); return; } } Linkedlist l2=head; while(l1!=null){ l1=l1.next; l2=l2.next; } System.out.println(l2.no); return; }
-
链表反转
思路是创建一个新的链表res,每次将链表从head链表中拿出一个节点,然后在res链表的第一个位置进行插入,就实现反转的功能,需要注意的是要先保留head.next的位置,最后再返还
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
public Linkedlist q3(Linkedlist head){ if(head==null){ System.out.println("链表为空"); return null; } Linkedlist res=new Linkedlist(0); head=head.next; while(head!=null){ Linkedlist node=head.next; head.next=res.next; res.next=head; head=node; } return res; }
-
从尾到头打印单链表
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
public void q4(Linkedlist linkedlist){ if(linkedlist==null){ System.out.println("null"); return; } Stack<Linkedlist> stack=new <Linkedlist> Stack(); Linkedlist temp=linkedlist.next; while(temp!=null){ stack.push(temp); temp=temp.next; } while(!stack.isEmpty()){ Linkedlist node= (Linkedlist) stack.pop(); System.out.println(node.no); } }
-
两个有序链表合并
两个链表在循环中比较大小然后进行插入,等一个链表遍历完之后,将另一个链表直接续上,这里需要注意的是,创建新链表是插入节点,不是直接更改temp的指向就可以的
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
public Linkedlist q5(Linkedlist l1,Linkedlist l2){ if(l1.next==null||l2.next==null){ if(l1.next==null&&l2.next==null){ System.out.println("两链表都为空"); return null; } else if (l1.next==null) { return l2; }else { return l1; } } Linkedlist r1=l1.next; Linkedlist r2=l2.next; Linkedlist res=new Linkedlist(0); Linkedlist temp=res; while(r1!=null&&r2!=null){ if(r1.no<r2.no){ Linkedlist node=r1.next; r1.next=temp.next; temp.next=r1; temp=temp.next; r1=node; }else { Linkedlist node=r2.next; r2.next=temp.next; temp.next=r2; temp=temp.next; r2=node; } } if(r1==null){ temp.next=r2; }else { temp.next=r1; } return res; }
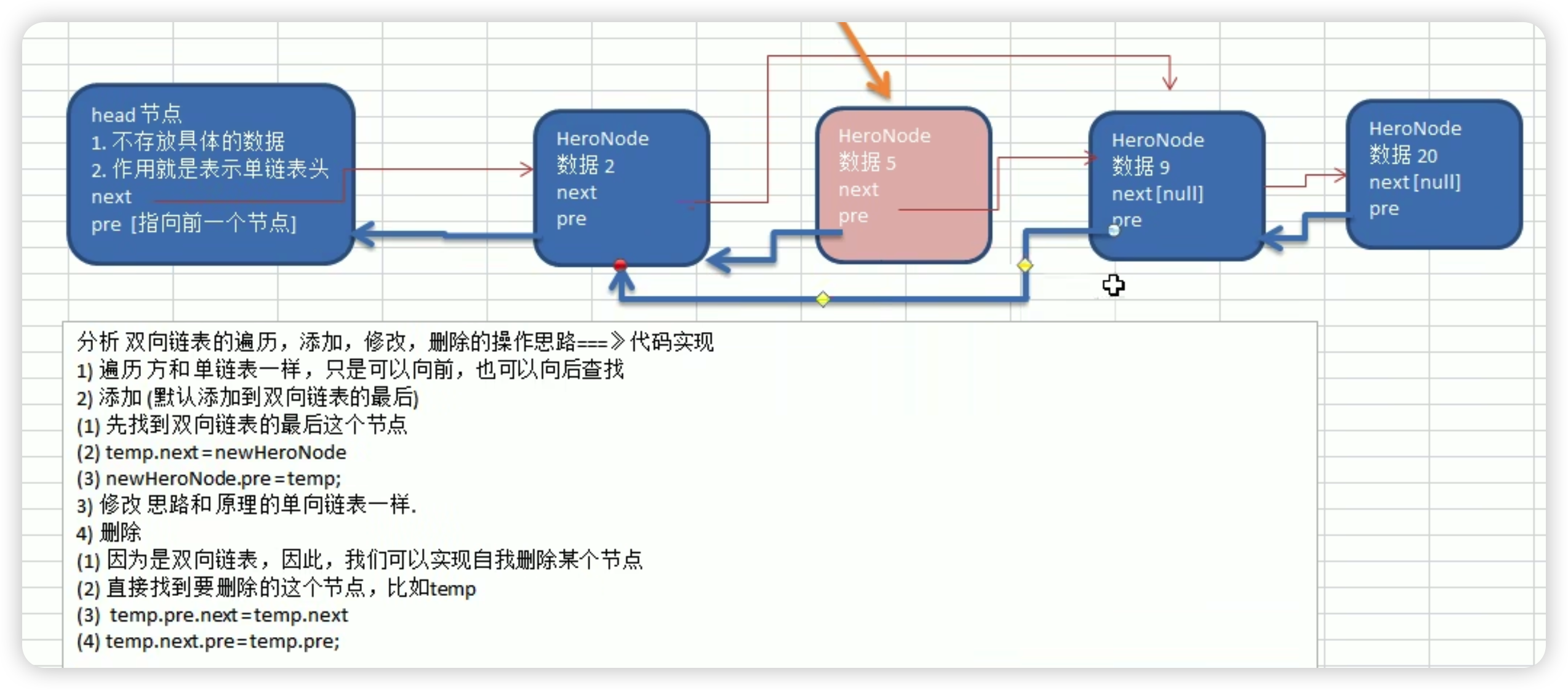
双向链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
package linkedlist;
public class doubleLinkedListDemo {
public static void main(String[] args) {
DoubleLinkedList head = new DoubleLinkedList(0);
DoubleLinkedList node2 = new DoubleLinkedList(2);
head.next = node2;
node2.pre = head;
DoubleLinkedList node3 = new DoubleLinkedList(3);
node2.next = node3;
node3.pre = node2;
DoubleLinkedList node=new DoubleLinkedList(5);
doubleLinkedListDemo dll = new doubleLinkedListDemo();
dll.insert(head,node,3);
dll.show(head);
}
//显示链表
public void show(DoubleLinkedList head){
if(head.next==null){
System.out.println("null");
return;
}
DoubleLinkedList temp=head.next;
while(temp!=null){
System.out.printf("%d\t",temp.no);
temp=temp.next;
}
return;
}
//默认添加到最后
public void add(DoubleLinkedList head,DoubleLinkedList node){
DoubleLinkedList temp=head.next;
while(temp!=null){
temp=temp.next;
}
temp.next=node;
node.pre=temp;
return;
}
//删除链表节点,比起单向链表要简单一些,不用再用temp.next来进行判断,不过就需要注意最后一个节点
public void delete(DoubleLinkedList head,int no){
if(head.next==null){
System.out.println("null");
return;
}
DoubleLinkedList temp=head.next;
while(temp!=null){
if(temp.no==no){
temp.pre.next=temp.next;
//因为和单链表不一样 不再是用temp.next进行判断,所以temp可以是最后一个节点
// 如果是最后一个节点则不能用temp.next.pre,这会是空指针异常
if(temp.next!=null)
temp.next.pre=temp.pre;
return;
}
temp=temp.next;
}
System.out.println("未找到该节点");
return;
}
public void insert(DoubleLinkedList head,DoubleLinkedList node,int no){
if(head.next==null){
System.out.println("null");
return;
}
DoubleLinkedList temp=head.next;
while(temp!=null){
if(temp.no==no){
node.next=temp.next;
node.pre=temp;
//同样的需要注意如果temp是最后一个节点,则需要注意空指针异常的问题
if(temp.next!=null)
temp.next.pre=node;
temp.next=node;
return;
}
temp=temp.next;
}
System.out.println("未找到");
return;
}
}
class DoubleLinkedList{
public int no;
public DoubleLinkedList pre;
public DoubleLinkedList next;
public DoubleLinkedList(int no){
this.no=no;
}
}
双向链表问题,比起单向链表多一个pre,在删除节点时简单一些,在插入中间节点时要难一些,主要是都要判断temp节点为最后一个节点时,temp.next.pre的空指针异常的问题
单向环形链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
package linkedlist;
public class Josepfu {
public static void main(String[] args) {
CircleSingleLinkedList circleSingleLinkedList=new CircleSingleLinkedList();
circleSingleLinkedList.addNode(25);
circleSingleLinkedList.showNode();
}
}
//创建一个node类
class Node{
public int no;
public Node next;
public Node(int no){
this.no=no;
}
}
//创建单向环形链表
class CircleSingleLinkedList{
private Node first=null;
public void addNode(int num){
//num表示需要创建节点的数量
if(num<1){
System.out.println("num不正确");
return;
}
//作为辅助节点 便于遍历
Node curNode=null;
for(int i=1;i<=num;i++){
//根据编号创建node节点
Node node=new Node(i);
//判断是否是第一个节点,如果是第一个节点需要先自己成一个环
if(i==1){
//让first指向第一个节点
first=node;
//让第一个节点先自己形成循环
node.next=node;
//让cur指向node 表示当前节点 便于添加新节点
curNode=node;
}
else{
//先将node加入链表中
curNode.next=node;
//让node指向头节点,形成环
node.next=first;
//让curNode移到当前节点
curNode=node;
}
}
return;
}
public void showNode(){
if(first==null){
System.out.println("环形链表为空");
return;
}
Node temp=first;
//需要先输出第一个,不然循环的条件就是temp.next!=first
// 如果这样 当temp为最后一个时进不了循环,无法输出最后一个节点
System.out.printf("%d\t",temp.no);
temp=temp.next;
while(temp!=first){
System.out.printf("%d\t",temp.no);
temp=temp.next;
}
}
}
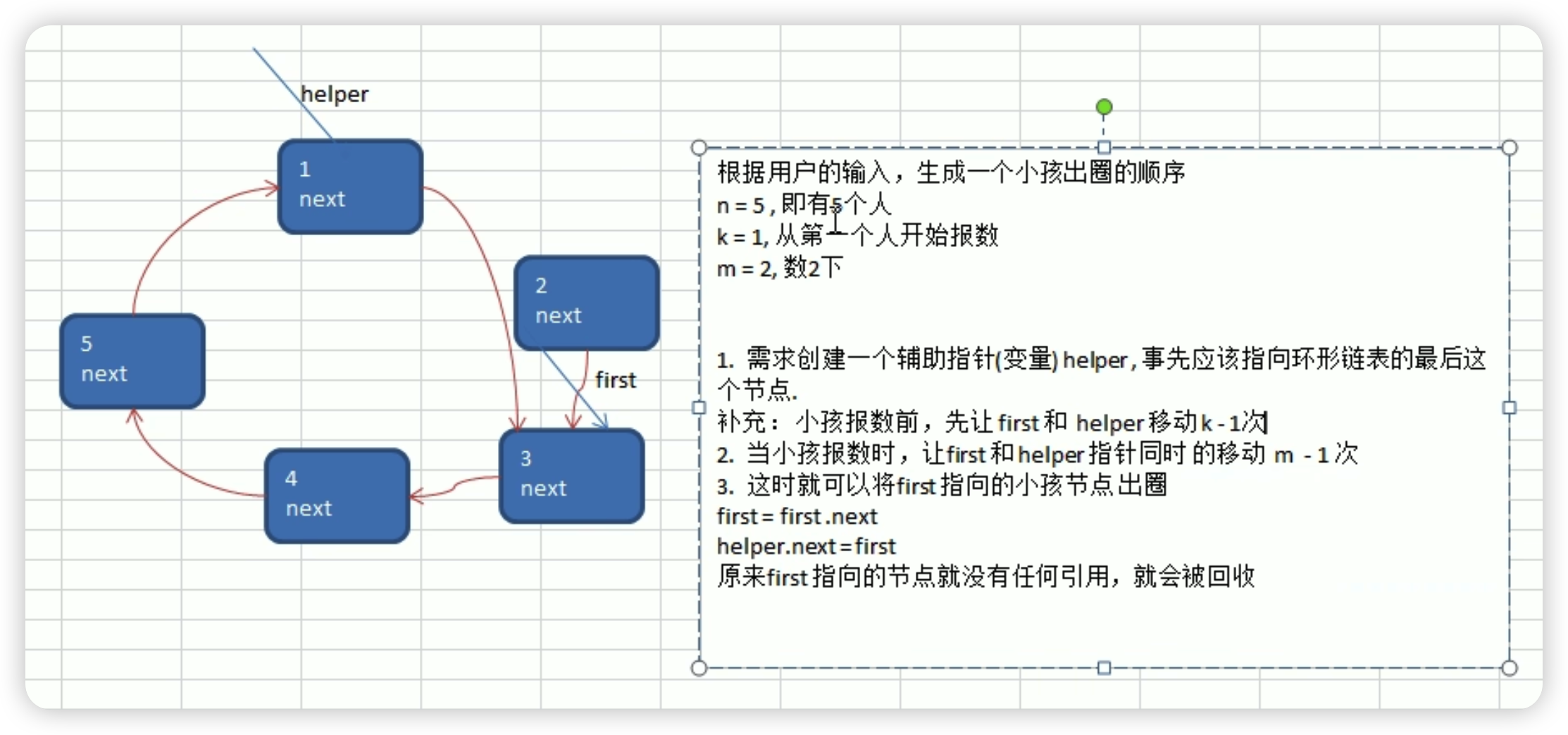
约瑟夫环
思路:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public void josepfu(int startNo,int countNum,int nums){
if(first==null||startNo<1||startNo>nums){
System.out.println("输入数据有误");
return;
}
//temp的作用是在delete的时候,起到在first前面的作用
Node temp=first;
//先通过下面循环让temp到first的前面一个
while(temp.next!=first)
temp=temp.next;
//通过这个循环,到指定的初始位置
for(int i=1;i<startNo;i++){
first=first.next;
temp=temp.next;
}
//通过下面的循环将除最后一个外的所有输出
while(first!=temp){
//先经过countnum个,让first到要输出的位置
for(int i=0;i<countNum;i++){
first=first.next;
temp=temp.next;
}
//进行输出
System.out.printf("%d\t",first.no);
//让first到下一个位置,然后让temp指向
// 相当于temp.next=temp.next.next
first=first.next;
temp.next=first;
}
System.out.printf("the last %d\t",first.no);
return;
}
栈
栈的基本操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class ArrayStack{
private int Maxsize;
private int []stack;
private int top=-1;
public void ArrayStack(int Maxsize){
this.Maxsize=Maxsize;
stack=new int[Maxsize];
}
public boolean isFull(){
return top==Maxsize-1;
}
public boolean isEmpty(){
return top==-1;
}
public void push(int a){
if(isFull()){
System.out.println("full");
return;
}
top++;
stack[top]=a;
}
public int pop(){
if(isEmpty()){
throw new RuntimeException("栈空");
}
int value=stack[top];
top--;
return value;
}
public void list(){
if(isEmpty()){
System.out.println("栈空");
return;
}
for(int i=top;i>-1;i--){
System.out.printf("%d\t",stack[i]);
}
return;
}
}
栈模拟计算器

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
package Stack;
public class Calculator {
public static void main(String[] args) {
String expression="4*(3+(5-9))";
arrayStack2 numStack=new arrayStack2(10);
arrayStack2 operStack=new arrayStack2(10);
int index=0;
int num1=0;
int num2=0;
int oper=0;
String countnum="";
while(index!=expression.length()){
char ch=expression.substring(index,index+1).charAt(0);
index++;
if(ch=='('){
operStack.push(ch);
}
else if(ch==')'){
while(operStack.peek()!='('){
num1=numStack.pop();
num2=numStack.pop();
oper=operStack.pop();
numStack.push(operStack.cal(num1,num2,oper));
}
operStack.pop();
}
//如果是字符
else if(operStack.ischar(ch)){
//如果为空 直接加入
if(operStack.isEmpty()){
operStack.push(ch);
}
else{
//判断当前符号优先级更低,则先把栈内优先级更高的拿出来计算
//如果是小于等于就要进行计算,不能存在优先级相等的运算符 考虑15/5*3 需要先计算15/5再计算*3 这样的话才可以用if即前面最多有一个优先级更大的
if(operStack.priority(ch)<=operStack.priority(operStack.peek())){
num1=numStack.pop();
num2=numStack.pop();
oper=operStack.pop();
numStack.push(operStack.cal(num1,num2,oper));
}
operStack.push(ch);
}
}
//如果是数字
else if(Character.isDigit(ch)){
//每一次给countcum清零
countnum="";
countnum+=ch;
while(index!=expression.length()&&Character.isDigit(expression.substring(index,index+1).charAt(0))){
ch=expression.substring(index,index+1).charAt(0);
countnum+=ch;
index++;
}
numStack.push(Integer.parseInt(countnum));
}
}
while(!operStack.isEmpty()){
num1=numStack.pop();
num2=numStack.pop();
oper=operStack.pop();
numStack.push(operStack.cal(num1,num2,oper));
}
System.out.println(numStack.pop());
return;
}
}
class arrayStack2 {
private int Maxsize;
private int []stack;
private int top=-1;
public arrayStack2(int Maxsize){
this.Maxsize=Maxsize;
stack=new int[Maxsize];
}
public boolean isFull(){
return top==Maxsize-1;
}
public boolean isEmpty(){
return top==-1;
}
public void push(int a){
if(isFull()){
System.out.println("full");
return;
}
top++;
stack[top]=a;
}
public int pop(){
if(isEmpty()){
throw new RuntimeException("栈空");
}
int value=stack[top];
top--;
return value;
}
public void list(){
if(isEmpty()){
System.out.println("栈空");
return;
}
for(int i=top;i>-1;i--){
System.out.printf("%d\t",stack[i]);
}
return;
}
public boolean ischar(int ch){
return ch=='+'||ch=='-'||ch=='*'||ch=='/';
}
//判断优先级
public int priority(int ch){
if(ch=='*'||ch=='/'){
return 1;
} else if (ch=='+'||ch=='-') {
return 0;
}
return -1;
}
public int peek(){
return stack[top];
}
public int cal(int num1,int num2,int oper){
int res=0;
switch (oper){
case '+':
res=num1+num2;
break;
case '-':
res=num2-num1;
break;
case '*':
res=num1*num2;
break;
case '/':
res=num2/num1;
}
return res;
}
}
栈的三种表达式
前缀表达式

中缀表达式

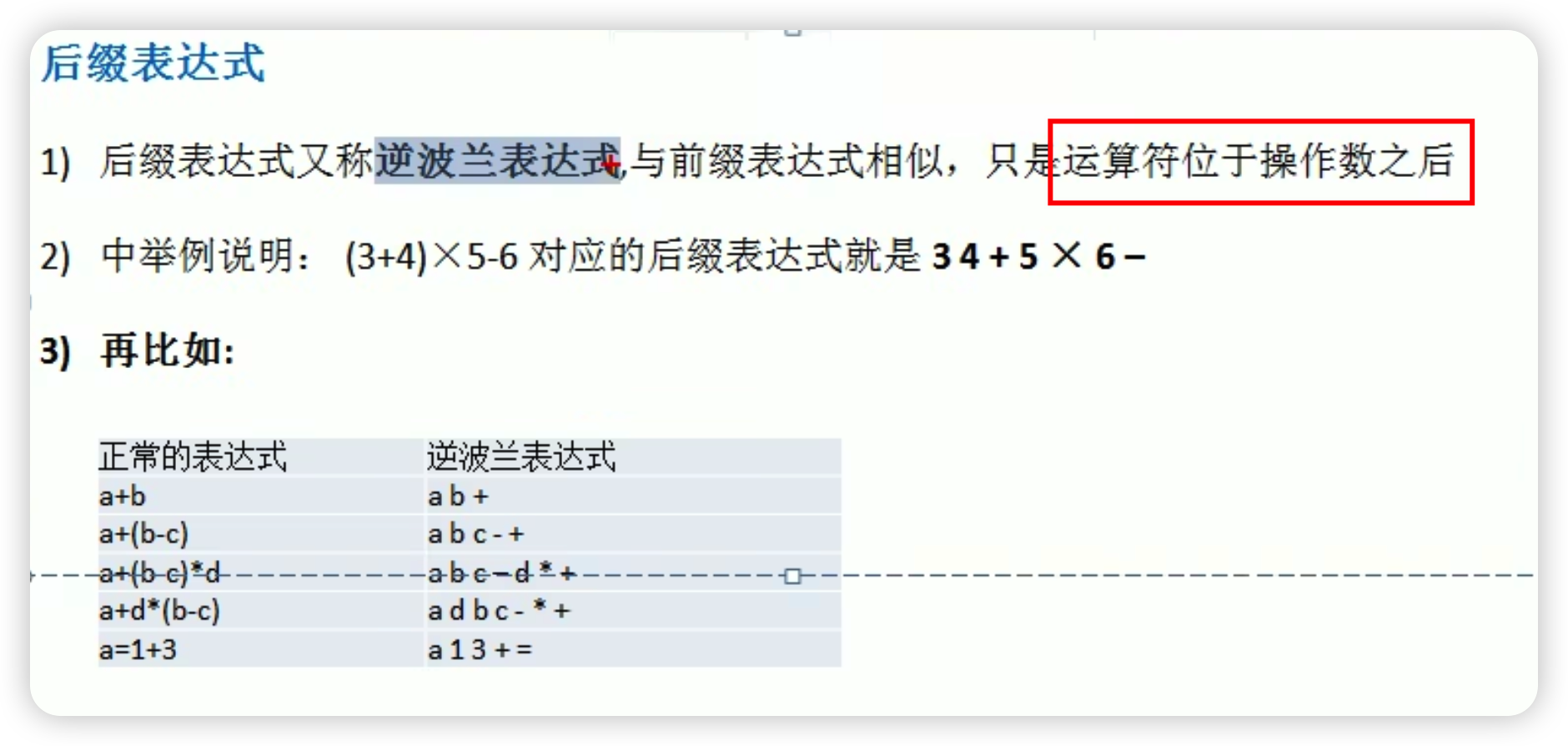
后缀表达式
逆波兰计算器
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
public class PolandNotation {
public static void main(String[] args) {
String Expression="3 4 + 5 * 6 -";
ArrayList<String>arrayList=StringToArrayList(Expression);
int res=cal(arrayList);
System.out.println(res);
}
public static ArrayList StringToArrayList(String Expression){
String []ch=Expression.split(" ");
ArrayList<String>arrayList=new ArrayList<>();
for(String element:ch){
arrayList.add(element);
}
return arrayList;
}
public static int cal(List<String>list){
Stack<String>stack=new Stack<>();
for(String item:list){
if(item.matches("\\d+")){
stack.push(item);
}
else{
int num1=Integer.parseInt(stack.pop());
int num2=Integer.parseInt(stack.pop());
int res=0;
switch (item){
case "+":
res=num1+num2;
break;
case "-":
res=num2-num1;
break;
case "*":
res=num1*num2;
break;
case "/":
res=num2/num1;
}
//res+"" 将整数转化成字符串
stack.push(res+"");
}
}
return Integer.parseInt(stack.peek());
}
}
中缀转后缀


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
package Stack;
import java.util.ArrayList;
import java.util.Collection;
import java.util.Collections;
import java.util.Stack;
public class InpixToPost {
//考虑的是表达式完全正确的情况下,且不出现其他运算符
public static void main(String[] args) {
String expression="1+((2+3)*4)-5";
ArrayList<String>arrayList=inpixtolist(expression);
System.out.println(IntoPost(arrayList));
}
public static ArrayList<String>IntoPost(ArrayList<String> arrayList){
ArrayList<String>res=new ArrayList<>();
//符号栈
Stack<String>s1=new Stack<>();
//暂存栈
Stack<String>s2=new Stack<>();
for(String item:arrayList){
//因为是字符串所以不能用==来判断字符串相等,应该用equals
if(isCharacter(item)){
//只有当前item优先级小于等于栈顶并且栈顶不为(并且栈不为空的时候需要将栈顶元素拿出,其余直接push
while(!s1.isEmpty()&&!s1.peek().equals("(")&&priority(item)<=priority(s1.peek())){
s2.push(s1.pop());
}
s1.push(item);
}else if(item.equals("(")){
s1.push(item);
}else if(item.equals(")")){
while(!s1.peek().equals("(")){
s2.push(s1.pop());
}
s1.pop();
}else {
s2.push(item);
}
}
//将s1剩下的倒入s2
while(!s1.isEmpty()){
s2.push(s1.pop());
}
//将s2中元入放入list中
while(!s2.isEmpty()){
res.add(s2.pop());
}
//进行反转
Collections.reverse(res);
return res;
}
public static ArrayList<String> inpixtolist(String expression){
int index=0;
String countnum="";
ArrayList<String>arrayList=new ArrayList<>();
while(index!=expression.length()){
char ch=expression.charAt(index);
index++;
if(Character.isDigit(ch)){
countnum="";
countnum+=ch;
while(index!=expression.length()&&Character.isDigit(expression.charAt(index))){
ch=expression.charAt(index);
countnum+=ch;
index++;
}
arrayList.add(countnum);
}else{
arrayList.add(ch+"");
}
}
return arrayList;
}
public static int priority(String ch){
if(ch.equals("+")||ch.equals("-"))
return 0;
if(ch.equals("*")||ch.equals("/"))
return 1;
return 0;
}
public static boolean isCharacter(String ch){
return ch.equals("+")||ch.equals("-")||ch.equals("*")||ch.equals("/");
}
}
递归
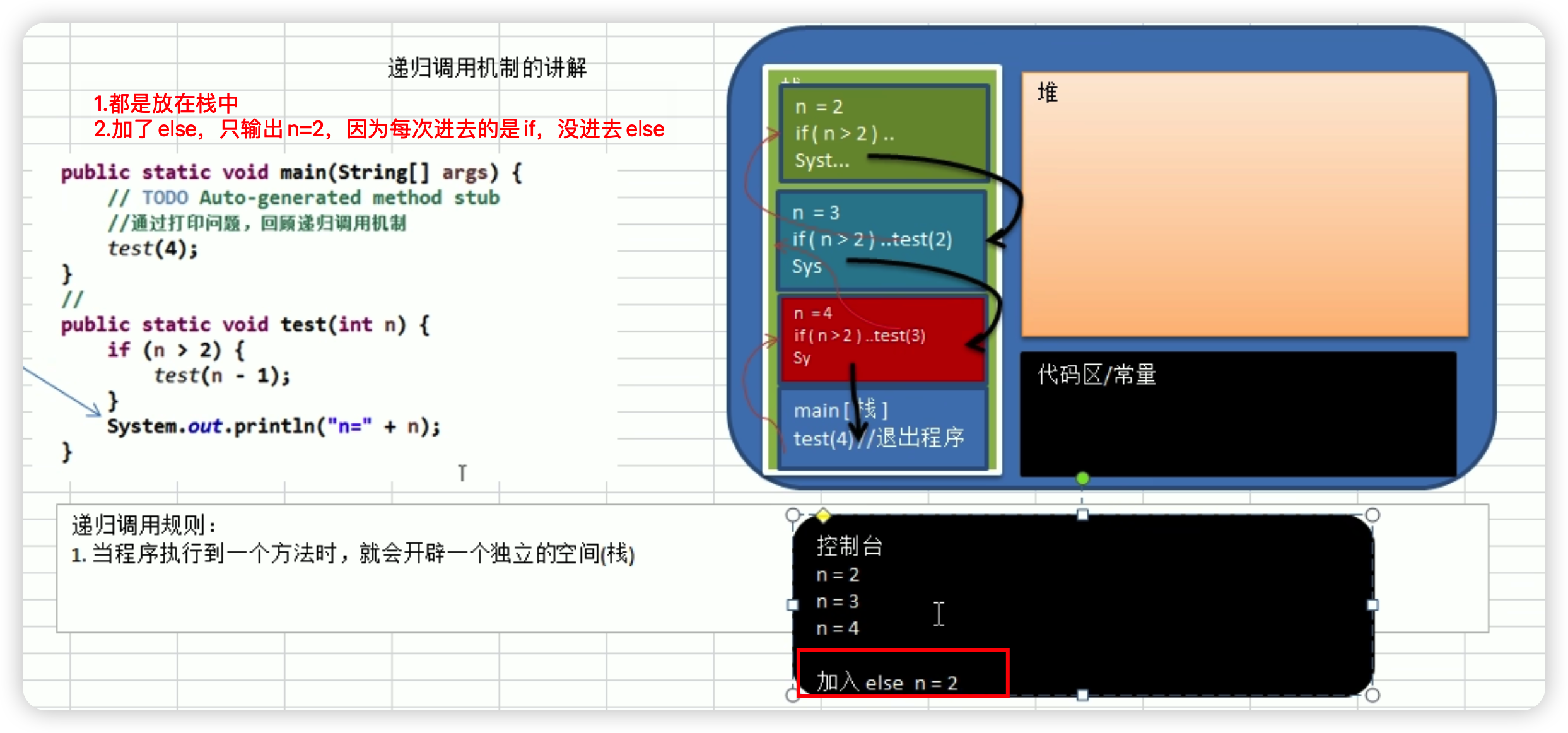

迷宫问题
用栈走出迷宫dfs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public static Stack<Integer> findway_stack(int maze[][], int i, int j){
int[][] visited=new int[maze.length][maze[0].length];
Stack<Integer>stack=new Stack<>();
Boolean flag=true;
stack.push(i);
stack.push(j);
int[][] directions={0,1},{1,0},{0,-1},{-1,0};
while(!stack.isEmpty()){
flag=false;
j=stack.pop();i=stack.pop();
if(i==maze.length-2&&j==maze[0].length-2){
stack.push(maze.length-2);stack.push(maze[0].length-2);
return stack;
}
stack.push(i);stack.push(j);
//将当前位置设置为已访问,只有在添加进栈的时候才需要去判断是否访问过
visited[i][j]=1;
for(int[] direction:directions){
int x=direction[0]+i;
int y=direction[1]+j;
if(x>=0&&x<maze.length&&y>=0&&y<maze[0].length&&maze[x][y]==0&&visited[x][y]!=1){
stack.push(x);
stack.push(y);
flag=true;
break;
}
}
//如果当前位置的下一步都不行,就把当前位置也丢掉
if(!flag){
stack.pop();stack.pop();
}
}
return new Stack<>();
}
用递归的方式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public static boolean set_way(int maze[][],int i,int j){
if(maze[maze.length-2][maze[0].length-2]==2){
return true;
}else{
if(maze[i][j]==0){
maze[i][j]=2;
if(set_way(maze,i+1,j)){
return true;
} else if (set_way(maze,i,j+1)) {
return true;
} else if (set_way(maze,i-1,j)) {
return true;
} else if (set_way(maze,i,j-1)) {
return true;
}else{
maze[i][j]=3;
return false;
}
}else{
return false;
}
}
}
八皇后问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
package recursion;
public class queue8 {
static int count;
public static void main(String[] args) {
//一共八个皇后
int max=8;
//定义一个数组用于记录解法
int []array=new int[max];
queue(array,0,max);
System.out.println("一共有:"+count+"解法");
}
public static void queue(int []array,int n,int max){
if(n==max){
print(array);
return;
}
for(int i=0;i<max;i++){
array[n]=i;
if(judge(array,n)){
queue(array,n+1,max);
}
}
}
public static boolean judge(int []array,int n){
for(int i=0;i<n;i++){
if(array[i]==array[n]||Math.abs(i-n)==Math.abs(array[i]-array[n])){
return false;
}
}
return true;
}
public static void print(int []array){
count++;
System.out.println("第"+count+"解法");
for(int arr:array){
System.out.print(arr+" ");
}
System.out.println();
}
}
复杂度
时间复杂度



排序
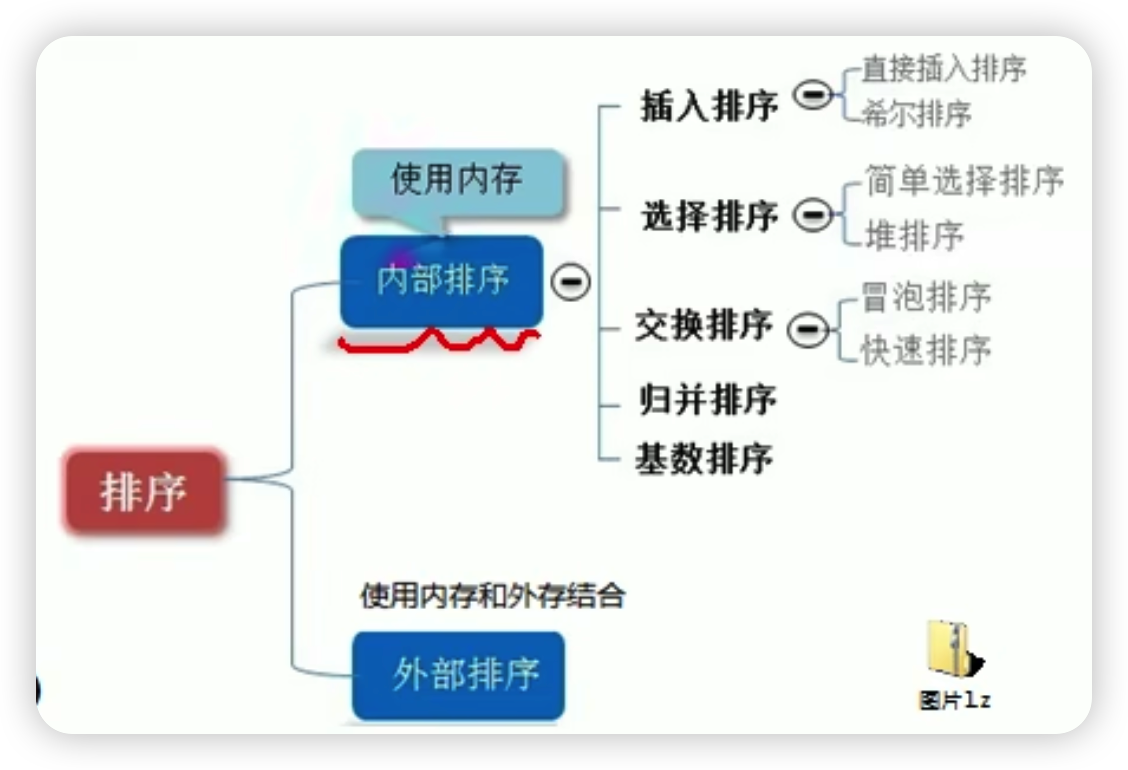
冒泡排序
相邻两个进行比较,所以可以用flag来简化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public static void Bubble(int []array){
int temp;
//如果某一次没有进行交换 说明已经有序
boolean flag=false;
for(int i=0;i<array.length-1;i++){
for(int j=0;j<array.length-i-1;j++){
if(array[j]>array[j+1]){
flag=true;
temp=array[j];
array[j]=array[j+1];
array[j+1]=temp;
}
}
if(flag)
flag=false;
else
break;
}
}
选择排序
每次选择剩下的序列中最大(最小)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public static void Select(int []array){
int num=0;
int temp;
for(int i=0;i<array.length-1;i++){
int max=-9999;
for(int j=0;j<array.length-i;j++){
//找到最大值,记录位置
if(array[j]>max){
num=j;
max=array[j];
}
}
//也可以进行判断 如果位置不同再进行交换
temp=array[num];
array[num]=array[array.length-i-1];
array[array.length-i-1]=temp;
}
}
插入排序
将整个序列分为前面的有序序列和后面的无序序列,从第二个开始向前插入,从前一个到0位置逐个判断,直到到0或者遇到比自己小的为止
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static void insert(int []array){
for(int i=1;i<array.length;i++){
//index表示当前要插入的为止
int index=i;
//因为插入是往后移动的,所以先将当前的保存下来
int temp=array[index];
while(index>0&&temp<array[index-1]){
//如果比前一个小,那么就将前面那个往后移动
array[index]=array[index-1];
index--;
}
array[index]=temp;
}
}
希尔排序
在插入排序的基础上进行的一个改进,根据gap=n/2对数组进行分组,然后对每个组进行插入排序,在重新分组再进行插入排序,直到gap=1最后进行一次插入排序
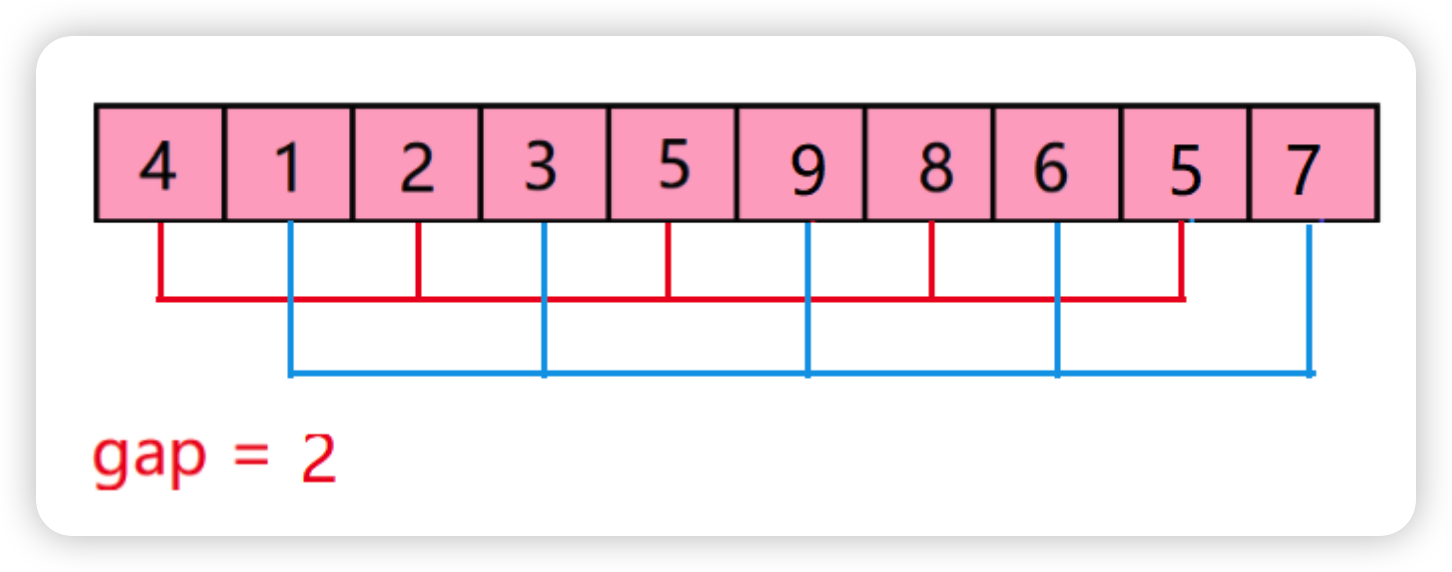
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static void shell(int []array){
//第一个for循环就是进行了那么多次的分组
for(int gap=array.length/2;gap>0;gap/=2){
//进行插入排序,不过不同的是i从gap开始,并且比较的数据是有gap间隔的,并且index判断条件是index>=gap
//这一个for循环,第一个组比如说是这样0 gap 2*gap 3*gap
//i自增到不同的值 不同的组进行一个插入排序
for(int i=gap;i<array.length;i++){
int index=i;
int temp=array[index];
while(index>=gap&&temp<array[index-gap]){
array[index]=array[index-gap];
index-=gap;
}
array[index]=temp;
}
}
}
快速排序

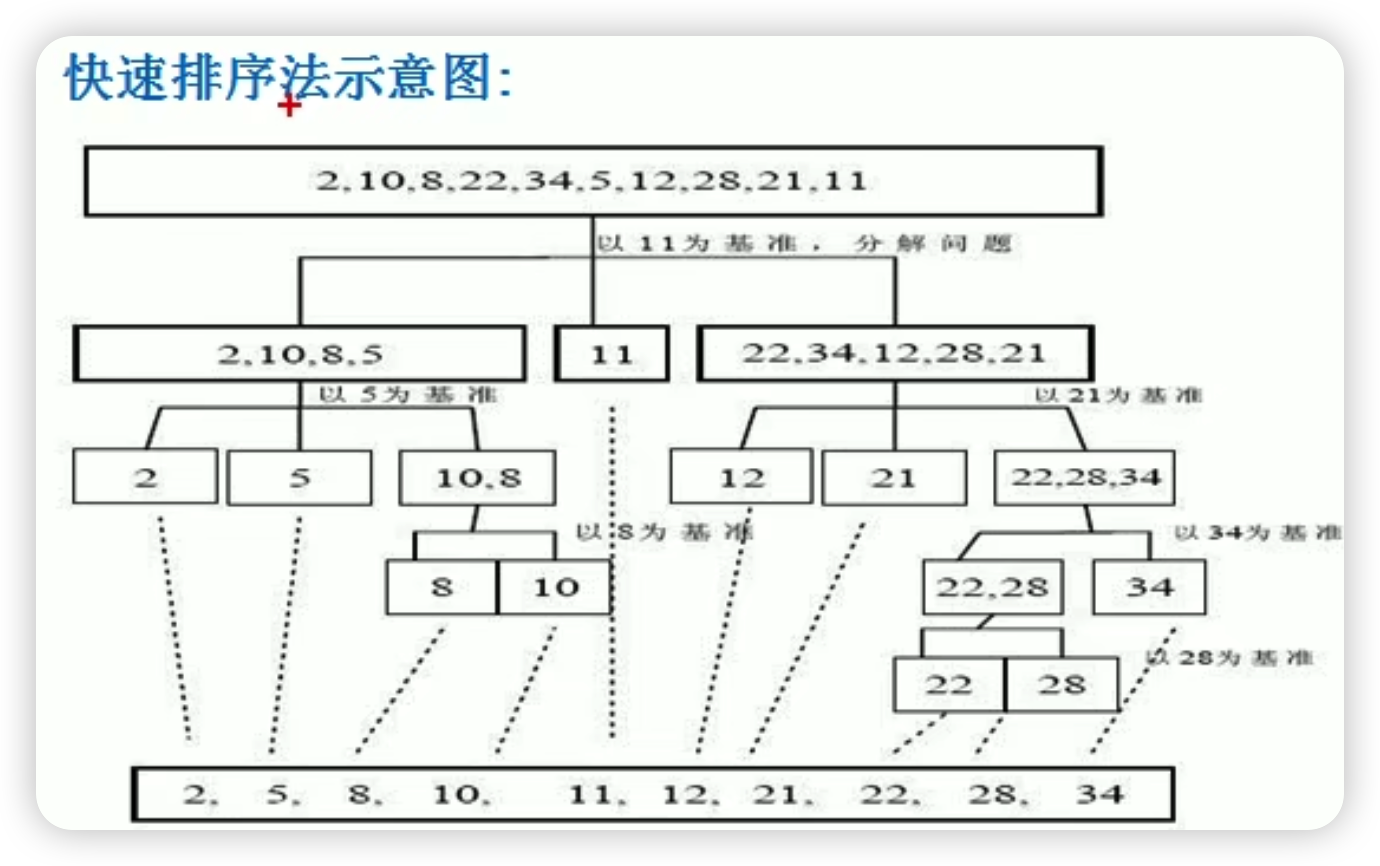
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public static void quick(int []array,int left,int right){
if(left>right)
return;
int start=left;int end=right;
//用左边第一个做为基准点
int pivot=array[start];
int temp;
while(start<end){
//要先从右往左,再从左往右,这样交换的时候才能保证中间点是小于等于基准点的
while(start<end&&array[end]>=pivot){
end--;
}
while(start<end&&array[start]<=pivot){
start++;
}
if(start<end){
temp=array[end];
array[end]=array[start];
array[start]=temp;
}
}
//循环出来一定是start==end的
//将排序一次后的中间点和基准点进行交换
array[left]=array[start];
array[start]=pivot;
quick(array,left,start-1);
quick(array,start+1,right);
}
归并排序
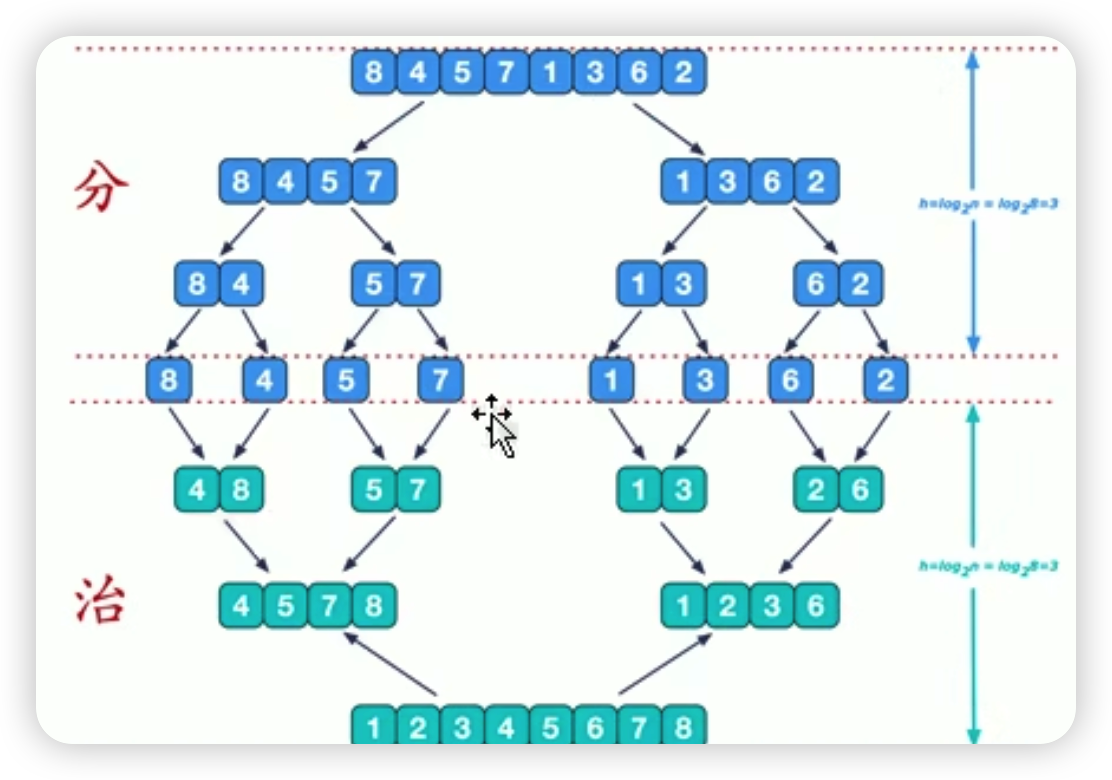
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public static void MergeSort(int []array,int left,int right){
if(left<right){
int mid=(left+right)/2;
//分治
MergeSort(array,left,mid);
MergeSort(array,mid+1,right);
//两有序数组融合
Merge(array,left,right,mid);
}
}
public static void Merge(int []array,int left,int right,int mid){
int num1=mid-left+1;
int num2=right-mid;
int arr1[]=new int[num1];
int arr2[]=new int[num2];
for(int i=0;i<num1;i++)
arr1[i]=array[left+i];
for(int i=0;i<num2;i++)
arr2[i]=array[mid+i+1];
int i=0,j=0,k=left;
while(i<num1&&j<num2){
//这里面不能用while,不然会越界
if(arr1[i]<=arr2[j]){
array[k++]=arr1[i++];
}else{
array[k++]=arr2[j++];
}
}
while(i<num1)
array[k++]=arr1[i++];
while(j<num2)
array[k++]=arr2[j++];
}
堆排序
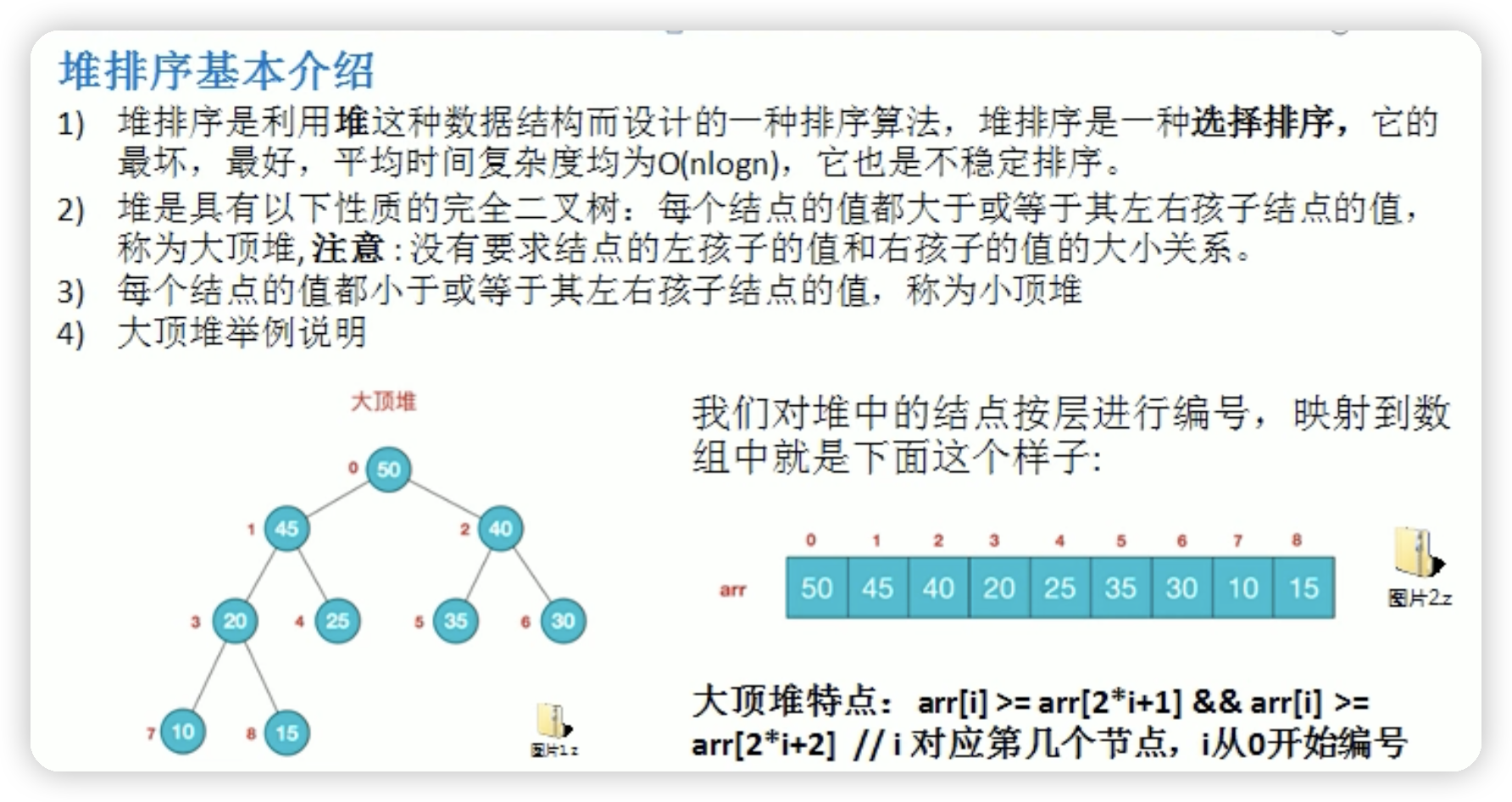
一般升序大顶堆 降序小顶堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public static void Heap(int []array){
//升序所以是大顶堆
//首先创建一个完整的大顶堆
//选择的i都是非叶子节点
for(int i=array.length/2-1;i>=0;i--){
AdjustHeap(array,i,array.length);
}
//然后对大顶堆进行抽取元素
int temp;
for(int j=array.length-1;j>0;j--){
//堆顶移到最后的位置不再参加堆排序
temp=array[j];
array[j]=array[0];
array[0]=temp;
//大顶堆已经建立好了 所以只需要在根节点提取就行了
AdjustHeap(array,0,j);
}
}
//i表示当前要调整的分支的根节点 选择的i都是非叶子节点 length表示当前还是无序的数组的长度
//堆排序是从下往上,从右往左
public static void AdjustHeap(int []arr,int i,int length){
int temp=arr[i];
//对于后面的根节点这种来说是需要循环的,排序的时候将根节点换下来
// 还要一直和后面的节点进行判断,如果还是更小就要继续往下沉
for(int k=i*2+1;k<length;k=k*2+1){
if(k+1<length&&arr[k]<arr[k+1]){
k++;
}
if(temp<arr[k]){
arr[i]=arr[k];
i=k;
}else {
//因为是从下往上进行的堆排序 所以当比两个子节点都大时,就不用再继续往下进行判断了
break;
}
}
arr[i]=temp;
}
基数排序
是一种非比较排序算法,适用于对整数进行排序。它的核心思想是从低位到高位逐渐对元素进行排序,通过多次按照某个位数进行分配和收集来达到排序的目的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
public static void Radix(int []array){
//创建list数组装填数据
LinkedList<Integer> list[]=new LinkedList[10];
for(int i=0;i<list.length;i++)
list[i]=new LinkedList<>();
for(int i=1;i<=getnum(array);i++){
//按照当轮位数分类
for(int j=0;j<array.length;j++){
list[getre(array[j],i)].offer(array[j]);
}
//合并
int num=0;
for(int k=0;k<list.length;k++){
while(!list[k].isEmpty()){
array[num++]=list[k].poll();
}
}
}
}
//获得循环的轮数
public static int getnum(int []array){
int max=array[0];
for(int arr:array){
if(max<arr)
max=arr;
}
return (max+"").length();
}
//得到每个数字在那一轮的位数
public static int getre(int num,int r){
int ret=0;
for(int i=0;i<r;i++){
ret=num%10;
num/=10;
}
return ret;
}
查找
二分查找
只针对于有序数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public static int binary(int []array,int num){
int mid;
int left=0,right=array.length-1;
while(left<=right){
mid=(left+right)/2;
if(array[mid]>num){
right=mid-1;
} else if (array[mid]<num) {
left=mid+1;
}else{
return mid;
}
}
return -1;
}
如果存在多个值相同的情况,因为是有序数组,所以向两边延伸判断即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public static ArrayList binary2(int []array, int num){
int left=0,right=array.length-1;
while(left<=right){
int mid=(left+right)/2;
if(array[mid]>num)
right=mid-1;
else if (array[mid]<num) {
left=mid+1;
}else {
ArrayList<Integer>arrayList=new ArrayList<>();
arrayList.add(mid);
int temp=mid-1;
while(temp>=0&&array[temp]==num){
arrayList.add(temp);
temp--;
}
temp=mid+1;
while(temp<array.length&&array[temp]==num){
arrayList.add(temp);
temp++;
}
return arrayList;
}
}
return null;
}
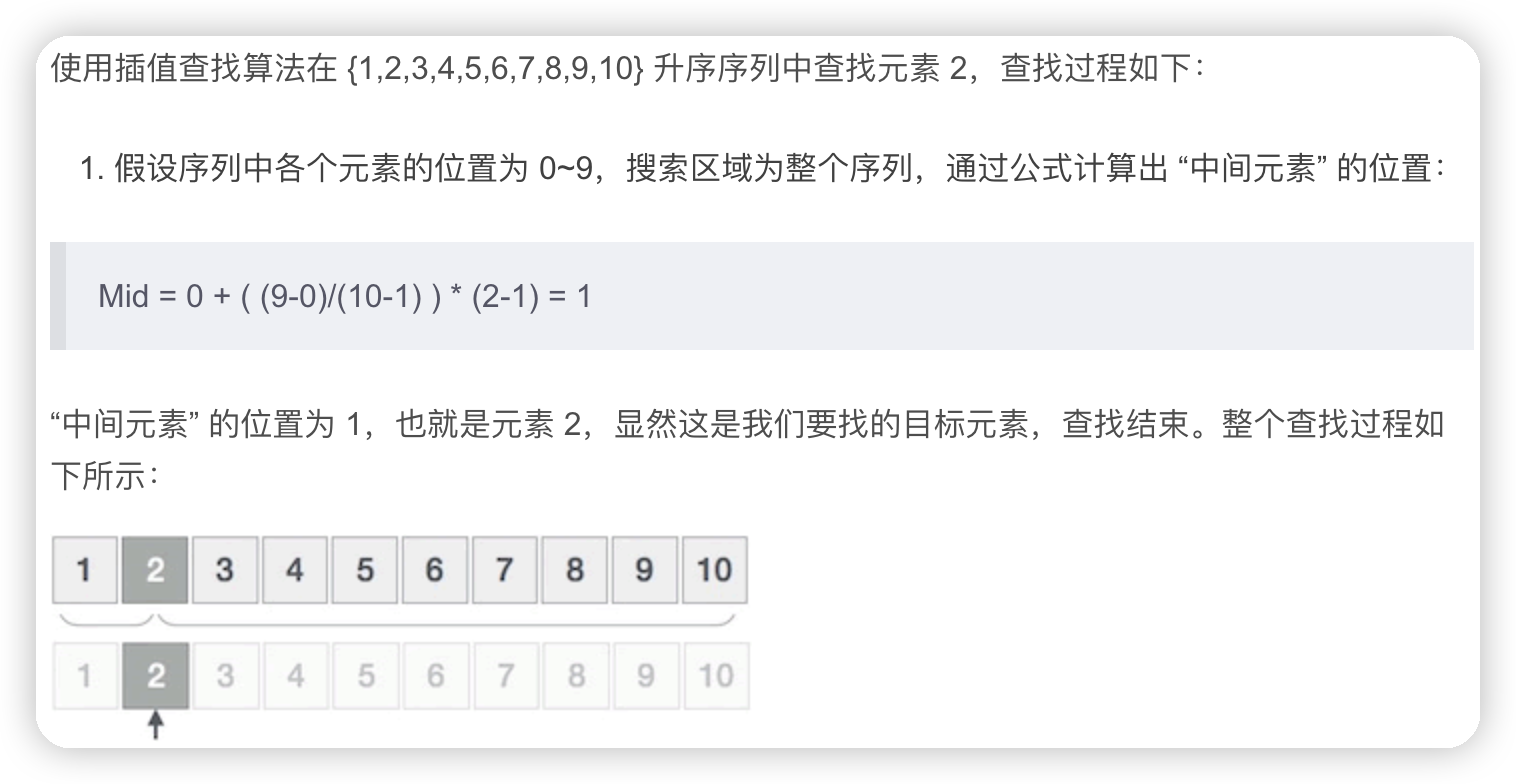
插值查找
和二分查找的区别就在mid的计算方式上,适用于大小分布均匀的序列,如10 20 30 40,查找的位置按照查找值的大小来确定
Mid = Begin + ( (End - Begin) / (A[End] - A[Begin]) ) * (X - A[Begin])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public static int Interpolation(int []array,int left,int right,int target){
if(left>right)
return -1;
if(left==right){
if(array[left]==target)
return left;
else
return -1;
}
int mid=left+(right-left)/(array[right]-array[left])*(target-array[left]);
if(array[mid]==target){
return mid;
} else if (array[mid]>target) {
return Interpolation(array,left,mid-1,target);
}else{
return Interpolation(array,mid+1,right,target);
}
}
斐波那契查找
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
public static int[] fib(int num){
int []array=new int[num];
array[0]=1;
array[1]=1;
for(int i=2;i<num;i++){
array[i]=array[i-1]+array[i-2];
}
return array;
}
public static int Fibonacci(int array[],int target){
int k=0;
int mid;
int []fib=fib(20);
while(array.length>fib[k]){
k++;
}
int left=0;int right=array.length-1;
int[] temp = Arrays.copyOf(array,fib[k]);
for(int i=right+1;i<temp.length;i++){
temp[i] = array[right];
}
while (left <= right) {
mid = left + fib[k - 1] - 1;
if(target<temp[mid]){
right = mid - 1;
k--;
}else if(target>temp[mid]){
left = mid +1;
k-=2;
}else{
if(mid<=right){
return mid;
}else{
return right;
}
}
}
return -1;
}
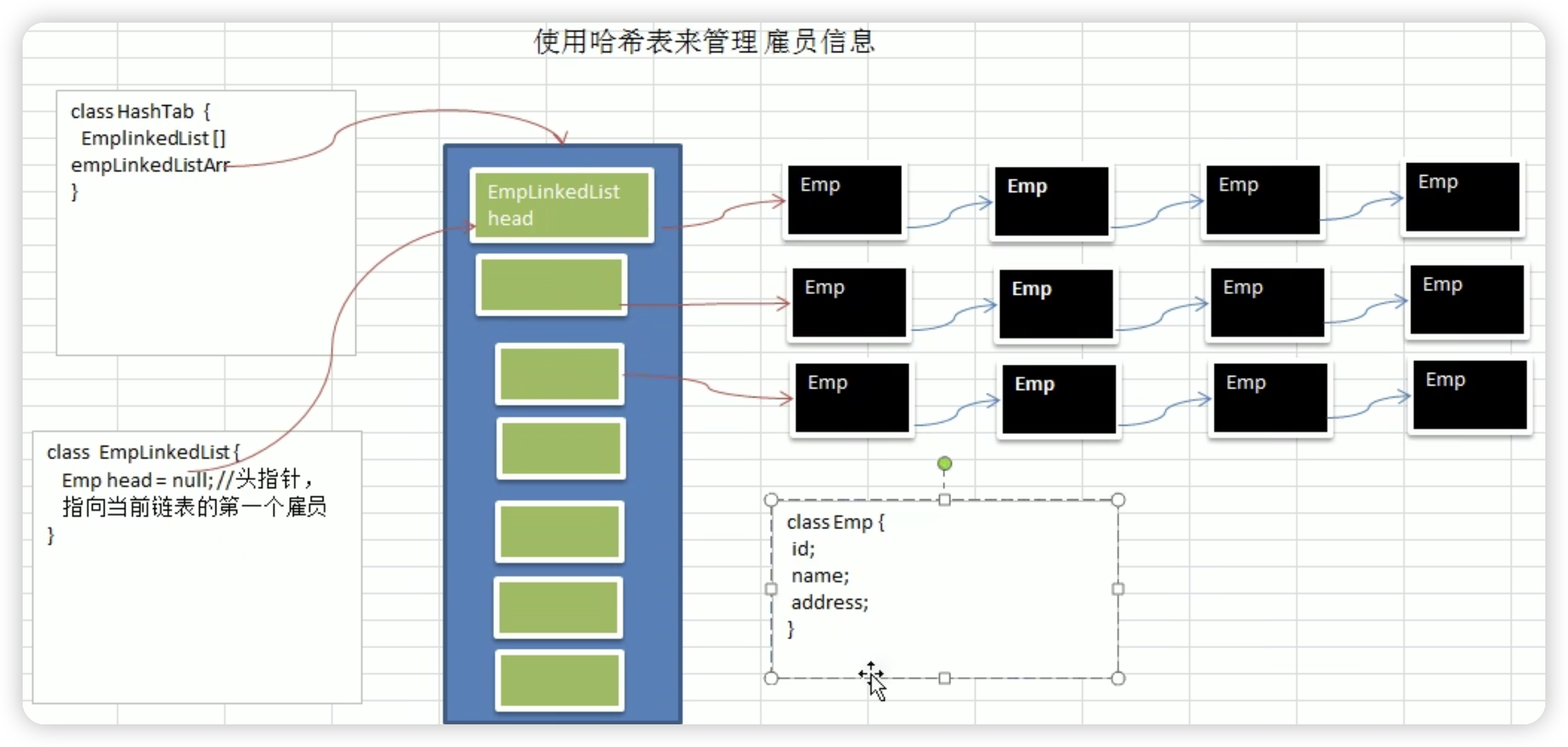
哈希表
它通过使用哈希函数将键映射到存储桶中,以实现高效的数据查找和插入。
哈希函数将输入的键转换成固定大小的哈希值,然后将该哈希值与存储空间的大小取模,得到一个索引值。根据这个索引值,可以将键值对存储在对应的存储桶(也称为哈希槽)中。
在使用哈希表进行查找时,通过哈希函数计算键对应的哈希值,然后根据哈希值找到对应的存储桶,并在该存储桶中查找目标值。由于哈希函数具有唯一性,因此在没有冲突的情况下,查找操作的时间复杂度为O(1)。但在存在冲突的情况下,多个键经过哈希函数计算得到相同的索引值,就会产生冲突。
应用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
class HashTable{
private EmpLinkedList[]empLinkedListsArray;
private int size;
public HashTable(int size){
this.size=size;
empLinkedListsArray=new EmpLinkedList[size];
for(int i=0;i<size;i++){
empLinkedListsArray[i]=new EmpLinkedList();
}
}
public void add(Emp emp){
int empNo=hashFun(emp.id);
empLinkedListsArray[empNo].add(emp);
}
public void List(){
for(int i=0;i<size;i++){
empLinkedListsArray[i].list();
}
}
//编写散列函数
public int hashFun(int id){
return id%size;
}
public void FindEmp(int id){
int empid=hashFun(id);
Emp emp=empLinkedListsArray[id].FindEmpById(id);
if(emp!=null){
System.out.println(emp.name);
}
}
}
//表示一个员工信息
class Emp{
public int id;
public String name;
public Emp next;
public Emp(int id, String name) {
this.id = id;
this.name = name;
}
}
//表示一条链表
class EmpLinkedList{
private Emp head=null;
public void add(Emp emp){
if(head==null){
head=emp;
return;
}
Emp temp=head;
while(temp.next!=null){
temp=temp.next;
}
temp.next=emp;
}
public void list(){
if(head==null)
System.out.println("null");
else{
Emp temp=head;
while(temp!=null){
System.out.print(temp.id+" ");
temp=temp.next;
}
System.out.println();
}
}
public Emp FindEmpById(int id){
if(head==null){
System.out.println("未找到");
return null;
}
Emp temp=head;
while(temp!=null){
if(temp.id==id){
return temp;
}
temp=temp.next;
}
System.out.println("未找到");
return null;
}
}
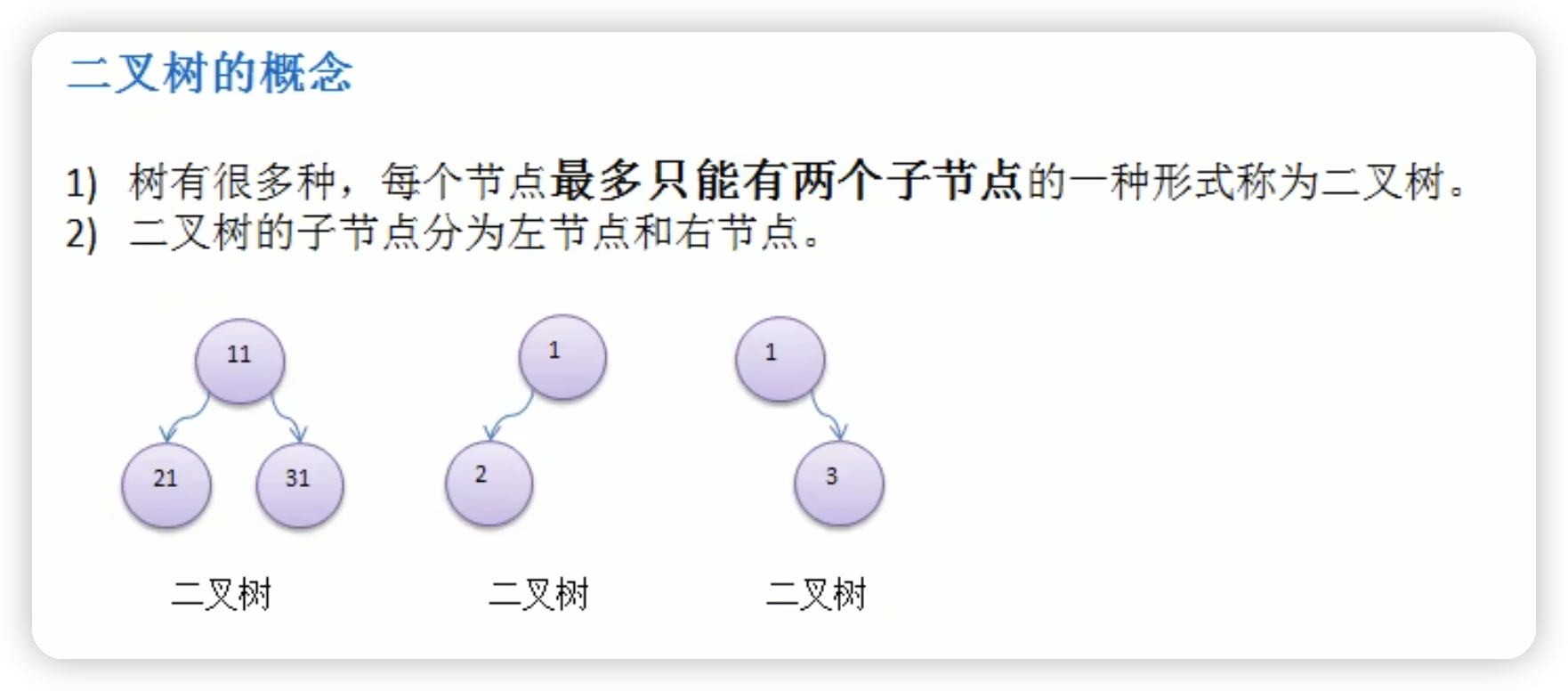
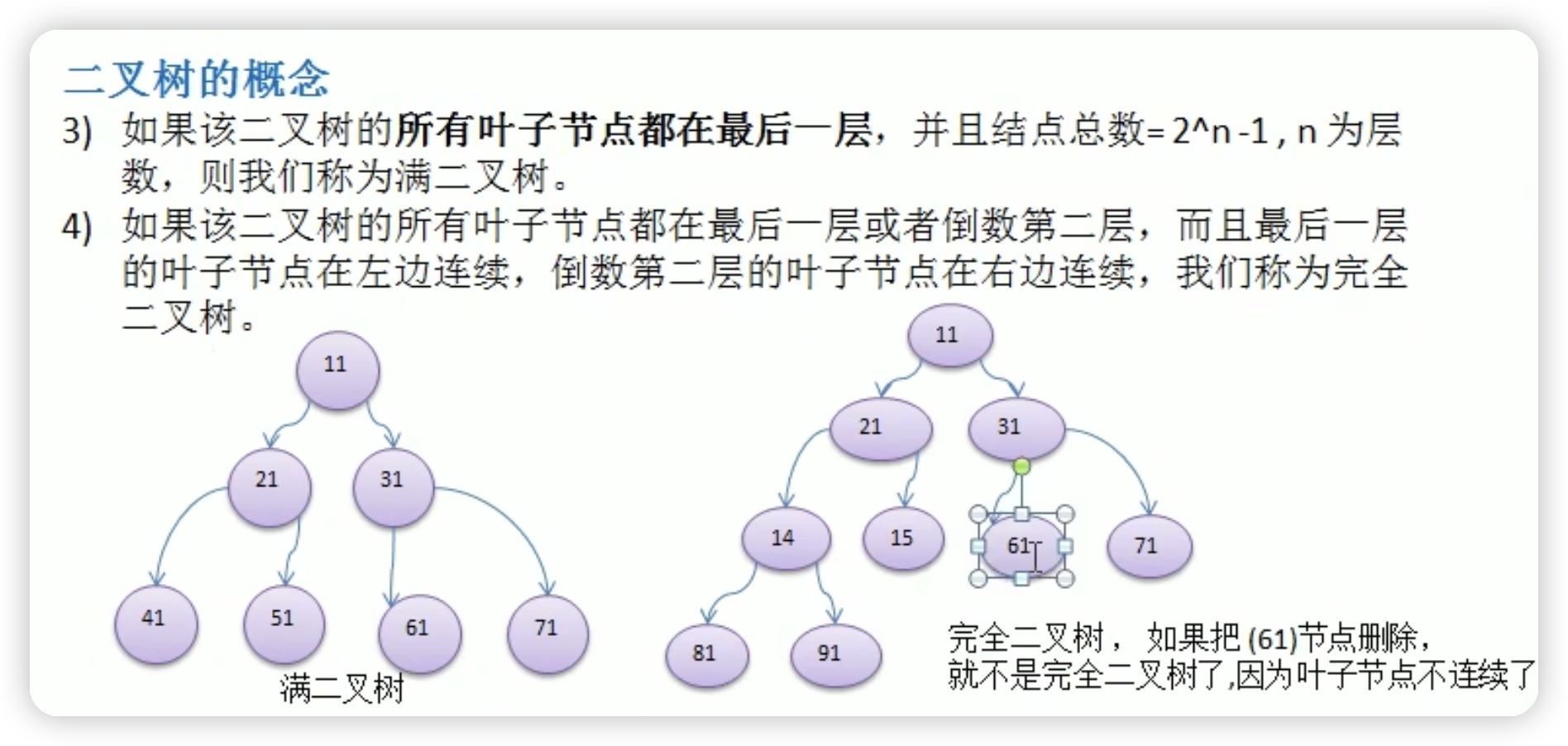
树

二叉树
二叉树前中后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Node {
int val;
Node left;
Node right;
public Node(int val) {
this.val = val;
this.left = null;
this.right = null;
}
}
public class BinaryTreeDemo {
public void preOrderTraversal(Node root) {
if (root == null) {
return;
}
System.out.print(root.val + " "); // 先访问根节点
preOrderTraversal(root.left); // 递归遍历左子树
preOrderTraversal(root.right); // 递归遍历右子树
}
public void inOrder(Node root){
if(root==null)
return;
inOrder(root.left);
System.out.println(root.val + " ");
inOrder(root.right);
}
public void postOrder(Node root){
if(root==null)
return;
postOrder(root.left);
postOrder(root.right);
System.out.println(root.val + " ");
}
public static void main(String[] args) {
// 构建二叉树
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
BinaryTreeDemo tree = new BinaryTreeDemo();
System.out.println("先序遍历结果:");
tree.preOrderTraversal(root);
}
}
前序遍历查找
1
2
3
4
5
6
7
8
9
public Node preOrderSearch(Node root,int no){
if(root==null||root.val==no)
return root;
Node res=preOrderSearch(root.left,no);
if(res!=null)
return res;
res=preOrderSearch(root.right,no);
return res;
}
删除节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public void del(Node root,int val){
if(root==null)
return;
if(root.val==val){
root=null;
return;
}
delNode(root,val);
}
public void delNode(Node root,int val){
if(root==null)
return;
if(root.left!=null&&root.left.val==val){
root.left=null;
return;
}
if(root.right!=null&&root.right.val==val){
root.right=null;
return;
}
delNode(root.left,val);
delNode(root.right,val);
}
顺序存储二叉树
对顺序存储二叉树进行前序遍历
即对数组进行前序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static void main(String[] args) {
// 构建二叉树
int []array={1,2,3,4,5,6,7};
ArrayBinaryTree arrayBinaryTree=new ArrayBinaryTree();
arrayBinaryTree.pre(array,0);
}
public void pre(int []array,int index){
if(array.length==0)
return;
System.out.print(array[index]+" ");
if(index*2+1<array.length){
pre(array,index*2+1);
}
if(index*2+2<array.length){
pre(array,index*2+2);
}
}
线索化二叉树
当线索化二叉树之后就不能用原来的方式进行遍历了,得进行一个判断
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
public class ThreadedBinaryTreeDemo {
public static void main(String[] args) {
// 创建一颗二叉树
TreeNode root = new TreeNode(4);
TreeNode node1 = new TreeNode(2);
TreeNode node2 = new TreeNode(6);
TreeNode node3 = new TreeNode(1);
TreeNode node4 = new TreeNode(3);
TreeNode node5 = new TreeNode(5);
TreeNode node6 = new TreeNode(7);
root.left = node1;
root.right = node2;
node1.left = node3;
node1.right = node4;
node2.left = node5;
node2.right = node6;
// 创建线索化二叉树对象
ThreadedBinaryTree threadedBinaryTree = new ThreadedBinaryTree();
threadedBinaryTree.setRoot(root);
// 进行线索化
threadedBinaryTree.threaded(root);
// 中序遍历线索化二叉树
System.out.println("中序遍历线索化二叉树:");
threadedBinaryTree.inorder();
}
}
class TreeNode {
int val;
TreeNode left;
TreeNode right;
//为0表示指向的是左右子树,为1表示指向的是前驱后驱节点
int leftType;
int rightType;
public TreeNode(int val) {
this.val = val;
this.left = null;
this.right = null;
}
}
class ThreadedBinaryTree {
private TreeNode root;
private TreeNode prev;
public void threaded(TreeNode node) {
if (node == null) {
return;
}
threaded(node.left);
//将前一个节点进行指向
if (node.left == null) {
node.left = prev;
node.leftType = 1;
}
//prev != null会轮空一次 等到下一个节点的时候才来判断后驱 因为在当前节点是不知道后面节点的位置,需要到了后面那个节点才能进行指向
if (prev != null && prev.right == null) {
prev.right = node;
prev.rightType = 1;
}
prev = node;
threaded(node.right);
}
public void inorder() {
TreeNode node = root;
while (node != null) {
//先到最左边的叶子节点
while (node.leftType==0) {
node = node.left;
}
//按照中序遍历的顺序应该进行输出
System.out.print(node.val + " ");
//输出之后就两种可能 要么有右子树要么没有右子树
//如果没有右子树那就是后驱节点 就一直进行输出 如果有右子树 那就转移到右子树上
while (node.rightType==1) {
node = node.right;
System.out.print(node.val + " ");
}
node = node.right;
}
}
public void setRoot(TreeNode root) {
this.root = root;
}
}
哈夫曼树

创建哈夫曼树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
public class huffmanTree {
public static void main(String[] args) {
int []array={13,7,8,3,29,6,1};
Node root=huffman(array);
root.preOrder(root);
}
public static Node huffman(int array[]){
ArrayList<Node>arrayList=new ArrayList<>();
for(int arr:array){
arrayList.add(new Node(arr));
}
while(arrayList.size()>1){
//首先对list里的节点大小进行排序
Collections.sort(arrayList);
//每次提取最小的两个进行相加创建新的节点
Node leftnode=arrayList.get(0);
Node rightnode=arrayList.get(1);
Node node=new Node(leftnode.val+ rightnode.val);
node.left=leftnode;node.right=rightnode;
arrayList.add(node);
arrayList.remove(leftnode);
arrayList.remove(rightnode);
}
return arrayList.get(0);
}
}
class Node implements Comparable<Node>{
int val;
Node left;
Node right;
public void preOrder(Node node){
if(node==null)
return;
System.out.print(node.val+" ");
preOrder(node.left);
preOrder(node.right);
}
public Node(int val) {
this.val = val;
}
@Override
public String toString() {
return "Node{" +
"val=" + val +
'}';
}
@Override
//加一个排序的功能
public int compareTo(Node o) {
//表示从小到大进行排序
return this.val-o.val;
}
}
哈夫曼编码

过程:将字符出现的频率作为权值,创建哈夫曼树,每一个叶子结点的路径就是这个字符的编码
这样的好处是
- 比起定长编码要更节省空间
- 因为每个字符都是叶子结点,所以路径都是唯一的 属于是前缀编码 不存在二义性
哈夫曼树不一定相同,因为如果存在权值相同的时候,就有可能造成不同
实践
编码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
package tree.huffmanTree;
import java.util.*;
public class huffmanCode {
public static void main(String[] args) {
String str="Huffman coding is a compression algorithm";
byte []bytes=str.getBytes();
//将字符串转化为一个list
List<nod>arrayList=getNodeList(bytes);
//通过list创建哈夫曼树
nod root=huffman(arrayList);
//对各个字符进行编码,创建哈夫曼表
getcode(root,"",stringBuilder);
//对byte数组进行编码后,再转化为byte
byte[]huffmancode=zip(bytes,huffmancodes);
System.out.println(Arrays.toString(huffmancode));
}
//对byte数组的每个字符进行频率统计,然后按照nod的格式存入list数组 这里需要用到map
private static List<nod> getNodeList(byte[]bytes){
List<nod>arrayList=new ArrayList<>();
Map<Byte,Integer>map=new HashMap<>();
for(byte b:bytes){
Integer count=map.get(b);
if(count==null){
map.put(b,1);
}else{
map.put(b,count+1);
}
}
for(Map.Entry<Byte,Integer> entry:map.entrySet()){
arrayList.add(new nod(entry.getKey(),entry.getValue()));
}
return arrayList;
}
//生成哈夫曼树
private static nod huffman(List<nod>nodes){
while(nodes.size()>1){
Collections.sort(nodes);
nod left=nodes.get(0);
nod right=nodes.get(1);
nod node=new nod(null, left.weight+ right.weight);
node.left=left;node.right=right;
nodes.add(node);
nodes.remove(left);nodes.remove(right);
}
return nodes.get(0);
}
//生成哈夫曼树编码表
//首先将哈夫曼编码表存储在map<Byte,String>的形式 Byte是字符的ascii String的字符的路径编码
static Map<Byte,String>huffmancodes=new HashMap<>();
//创建一个StringBuilder来拼接字符的路径
static StringBuilder stringBuilder=new StringBuilder();
private static void getcode(nod root,String code,StringBuilder stringBuilder){
if(root==null)
return;
StringBuilder stringBuilder1=new StringBuilder(stringBuilder);
stringBuilder1.append(code);
if(root.val==null){
getcode(root.left,"0",stringBuilder1);
getcode(root.right,"1",stringBuilder1);
}else {
huffmancodes.put(root.val,stringBuilder1.toString());
}
}
//对byte数组进行编码生成二进制编码,然后再将二进制编码转化为byte数组
private static byte[] zip(byte[]bytes,Map<Byte,String>huffmancodes){
StringBuilder stringBuilder1=new StringBuilder();
//根据哈夫曼表将要压缩的字符串转化为二进制编码
for(byte b:bytes){
stringBuilder1.append(huffmancodes.get(b));
}
//将这堆二进制编码转化为byte数组,首先求数组的长度
int len=(stringBuilder1.length()+7)/8;
byte huffmancode[]=new byte[len];
int index=0;
for(int i=0;i<stringBuilder1.length();i+=8){
String strByte;
//最后的部分不一定满8个 所以要进行判断
if(i+8>stringBuilder1.length()){
strByte=stringBuilder1.substring(i);
}else{
strByte=stringBuilder1.substring(i,i+8);
}
//提取八位数之后进行转化
huffmancode[index++]= (byte) Integer.parseInt(strByte,2);
}
return huffmancode;
}
}
class nod implements Comparable<nod>{
Integer weight; //字符出现的频率
Byte val; //存放数据本身
nod left;
nod right;
public nod(Byte val,Integer weight) {
this.weight = weight;
this.val = val;
}
@Override
public String toString() {
return "node{" +
"weight=" + weight +
", val=" + val +
'}';
}
@Override
public int compareTo(nod o) {
return this.weight-o.weight;
}
}
解码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
//5.解压
//5.1首先将数组转化为二进制字符串
private static String bytetoString(boolean flag,Byte b){
int temp=b;
//flag用于判断是否要补高位数如果是正数就要补高位 flag用于判断是不是最后一个byte,因为最后一个byte位数不一定是8 不一定需要补齐
if(flag)
temp|=256;
String str=Integer.toBinaryString(temp);
if(flag)
//因为是int 更长 所以取后八位
return str.substring(str.length()-8);
else
return str;
}
//5.2对照哈夫曼表进行翻译
private static byte[] decode(Map<Byte,String>huffmancodes,byte[]huffmancode){
StringBuilder stringBuilder1=new StringBuilder();
for(int i=0;i<huffmancode.length;i++){
if(i!=huffmancode.length-1){
stringBuilder1.append(bytetoString(true,huffmancode[i]));
}else
stringBuilder1.append(bytetoString(false,huffmancode[i]));
}
//把二进制编码转化成字符
//为了方便翻译,将哈夫曼编码表key和value进行交换
Map<String,Byte>map=new HashMap<>();
for(Map.Entry<Byte,String>entry:huffmancodes.entrySet()){
map.put(entry.getValue(),entry.getKey());
}
List<Byte>list=new ArrayList<>();
for(int i=0;i<stringBuilder1.length();){
int count=0;
Boolean flag=true;
Byte b=null;
while (b==null){
count++;
String str=stringBuilder1.substring(i,i+count);
b=map.get(str);
}
list.add(b);
i+=count;
}
byte []res=new byte[list.size()];
for(int i=0;i<list.size();i++){
res[i]=list.get(i);
}
return res;
}
文件压缩
二叉排序树

添加节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public void add(Node node){
if(node==null)
return;
if(node.val<this.val){
if(this.left==null)
this.left=node;
else
this.left.add(node);
}else{
if(this.right==null)
this.right=node;
else
this.right.add(node);
}
}
删除节点

对于第三种情况,先得到该节点的右子树的最小值的节点,获取该值,然后进行删除右子树最小节点,在将该值赋给该节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
package tree.BST;
public class BST {
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree();
// 插入节点
bst.insert(5);
bst.insert(3);
bst.insert(7);
bst.insert(2);
bst.insert(4);
// 删除节点
System.out.println("删除前的二叉排序树:");
inorderTraversal(bst.root); // 中序遍历二叉排序树
bst.delete(2);
System.out.println();
System.out.println("删除后的二叉排序树:");
inorderTraversal(bst.root); // 中序遍历二叉排序树
}
private static void inorderTraversal(TreeNode root) {
if (root == null) {
return;
}
inorderTraversal(root.left);
System.out.print(root.val + " ");
inorderTraversal(root.right);
}
}
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
TreeNode root;
public BinarySearchTree() {
this.root = null;
}
public void insert(int val) {
root = insertNode(root, val);
}
private TreeNode insertNode(TreeNode root, int val) {
if (root == null) {
return new TreeNode(val);
}
if (val < root.val) {
root.left = insertNode(root.left, val);
} else if (val > root.val) {
root.right = insertNode(root.right, val);
}
return root;
}
public void delete(int val) {
root = deleteNode(root, val);
}
private TreeNode deleteNode(TreeNode root, int val) {
if (root == null) {
return null;
}
if (val < root.val) {
root.left = deleteNode(root.left, val);
} else if (val > root.val) {
root.right = deleteNode(root.right, val);
} else { // 找到要删除的节点
if (root.left == null && root.right == null) {
// 情况1:要删除的节点为叶子节点
return null; // 返回 null 断开对该节点的引用
} else if (root.left == null || root.right == null) {
// 情况2:要删除的节点只有左子树或右子树
return (root.left != null) ? root.left : root.right;
} else {
// 情况3:要删除的节点既有左子树又有右子树
TreeNode predecessor = findMax(root.left); // 找到前驱节点(左子树的最大节点)
root.val = predecessor.val; // 使用前驱节点替代要删除的节点的值
root.left = deleteNode(root.left, predecessor.val); // 递归地在左子树中删除前驱节点
}
}
return root;
}
private TreeNode findMax(TreeNode node) {
while (node.right != null) {
node = node.right;
}
return node;
}
}
平衡二叉树
二叉排序树的缺点

平衡二叉树特点

创建平衡二叉树

将节点6设置为根节点,然后将5设置为4的右子树,这样右边的高度减1,左边的高度加1
左旋操作
1
2
3
4
5
6
7
8
9
10
11
public TreeNode leftRotate(TreeNode root){
//1.创建一个和根节点相同大小的节点
TreeNode node=new TreeNode(root.val);
node.left=root.left;
//因为要将右子节点作为根节点,所以右子节点的左子树得划到左边
node.right=root.right.left;
//让右子节点指向新节点
root.right.left=node;
//让右子节点作为根节点
return root.right;
}
右旋转操作
1
2
3
4
5
6
7
public TreeNode rightRotate(TreeNode root){
TreeNode node=new TreeNode(root.val);
node.right=root.right;
node.left=root.left.right;
root.left.right=node;
return root.left;
}
但单纯在插入节点方法中调用上面两个方法是不够的,考虑下面这种情况

这样的情况是因为左子树的右子树太长了 移到右边后 就会导致右边又更长了 所以得保证左子树的左子节点长度不小于右子节点的长度 所以要进行判断
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
private TreeNode insertNode(TreeNode root, int val) {
if (root == null) {
return new TreeNode(val);
}
if (val < root.val) {
root.left = insertNode(root.left, val);
} else if (val > root.val) {
root.right = insertNode(root.right, val);
}
//左旋转 添加完节点后 右子树的高度与左子树高度之差大于1
//因为有对根节点的操作,而在其他方法里对根节点的引用进行更改是没用的,所以需要一个赋值,将该地址返回给原方法的根节点
if(height(root.right)>(height(root.left)+1)){
if(height(root.right.left)>height(root.right.right))
root.right=rightRotate(root.right);
root=leftRotate(root);
}else if(height(root.left)>(height(root.right)+1)){
if(height(root.left.right)>height(root.left.left))
root.left=leftRotate(root.left);
root=rightRotate(root);
}
return root;
}
多路查找树

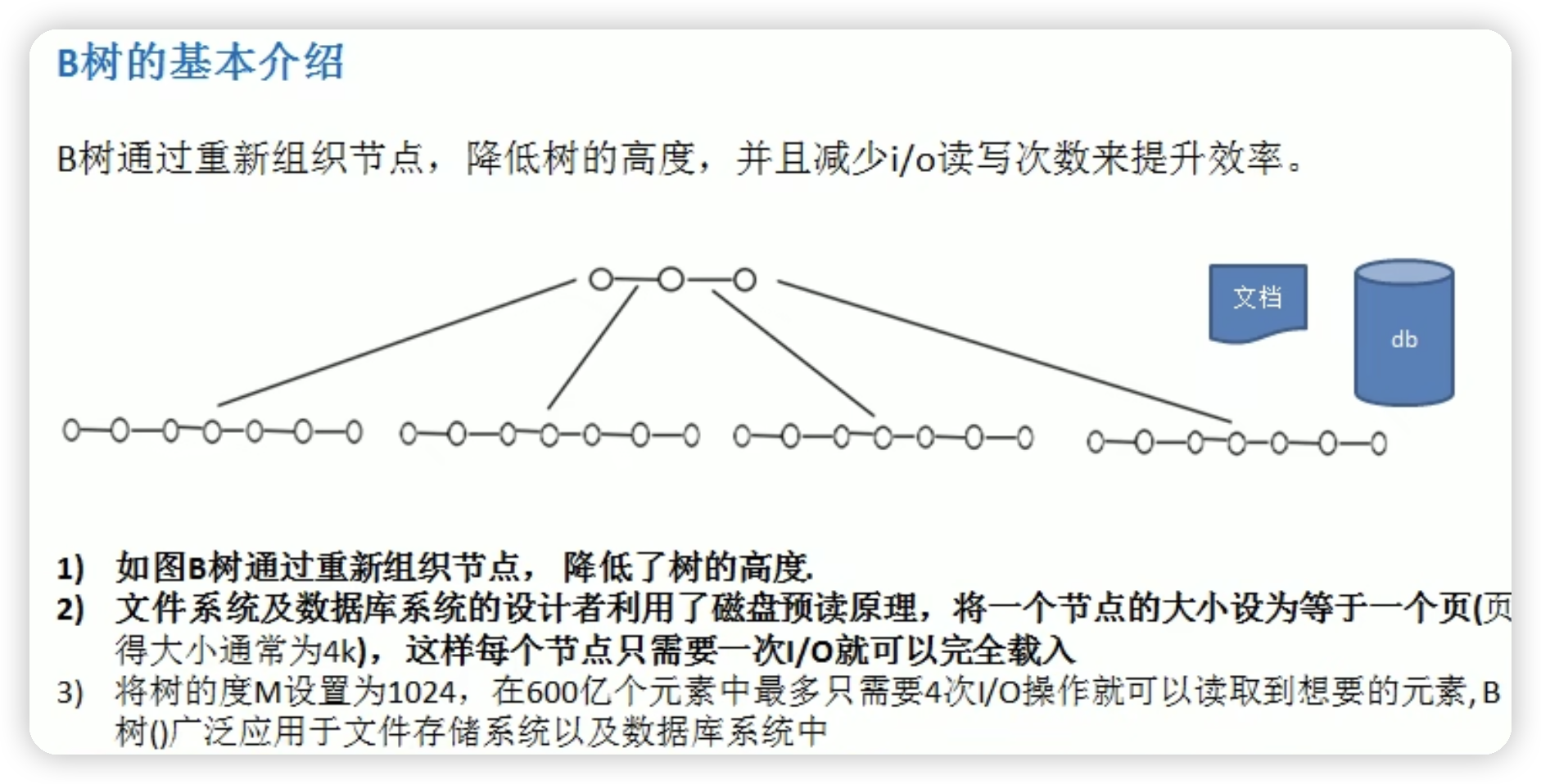
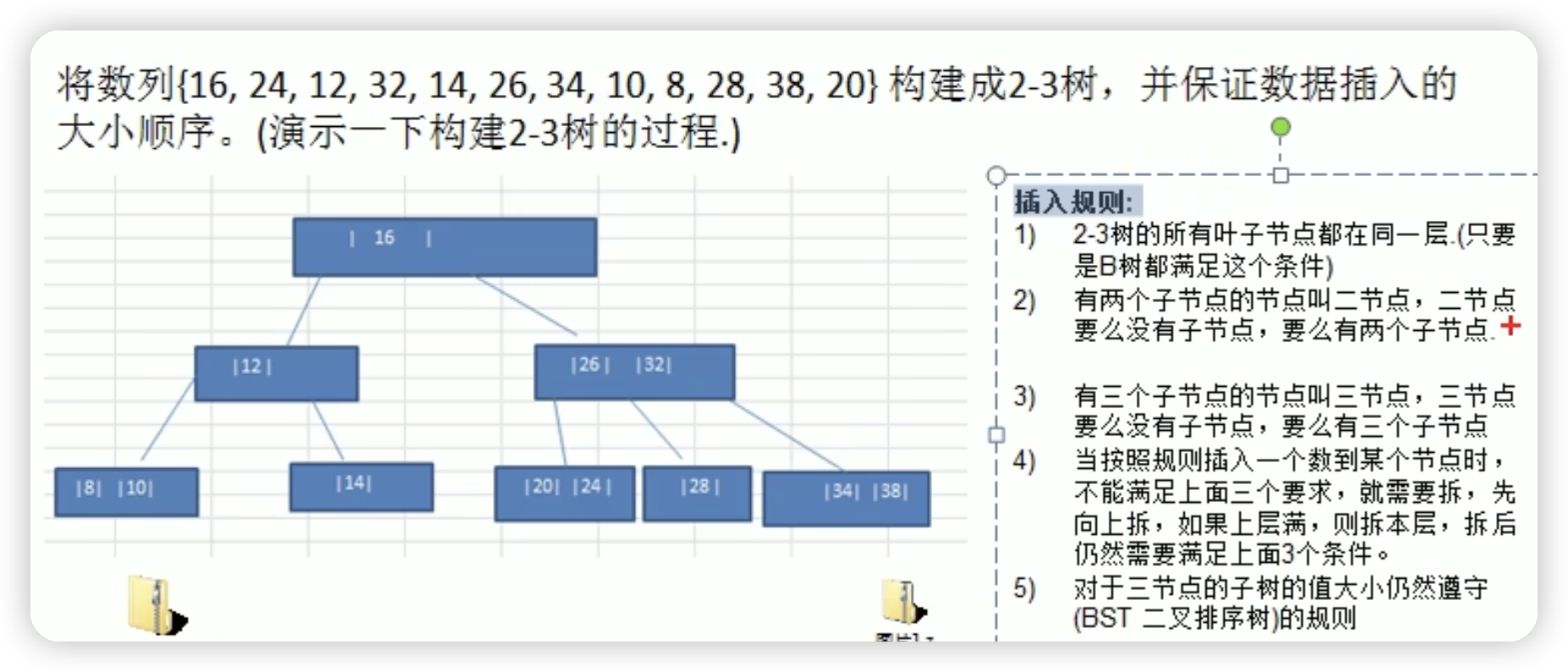
2-3树

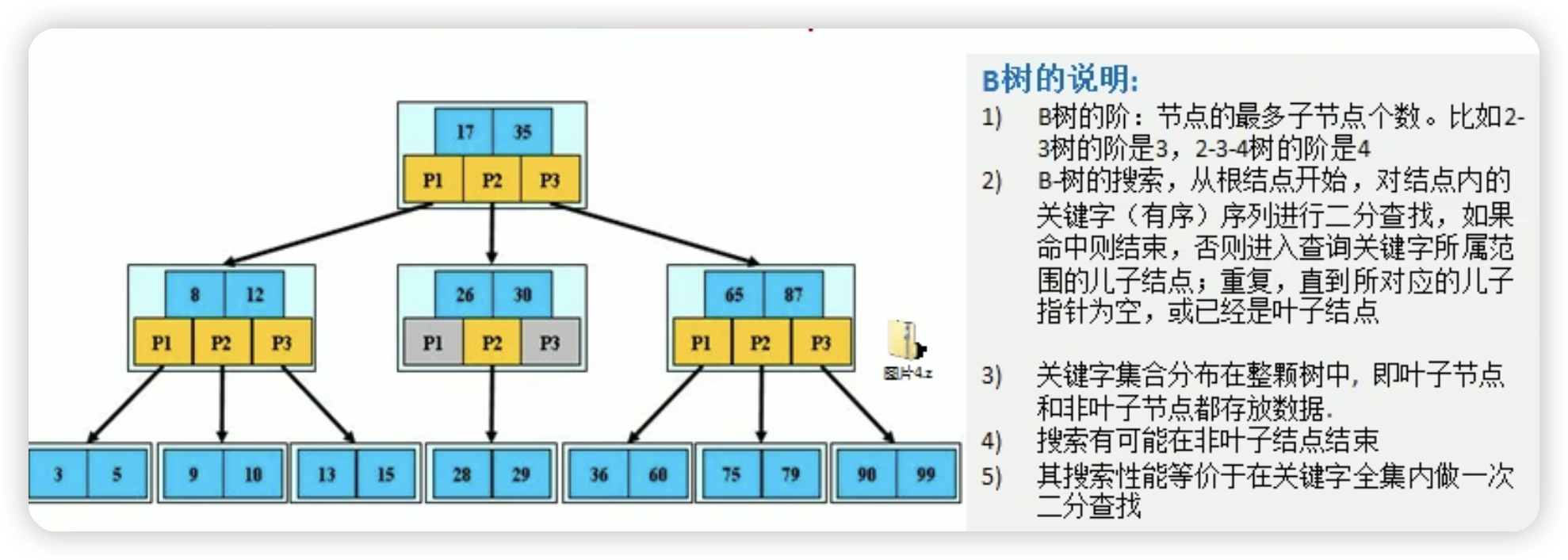
B树
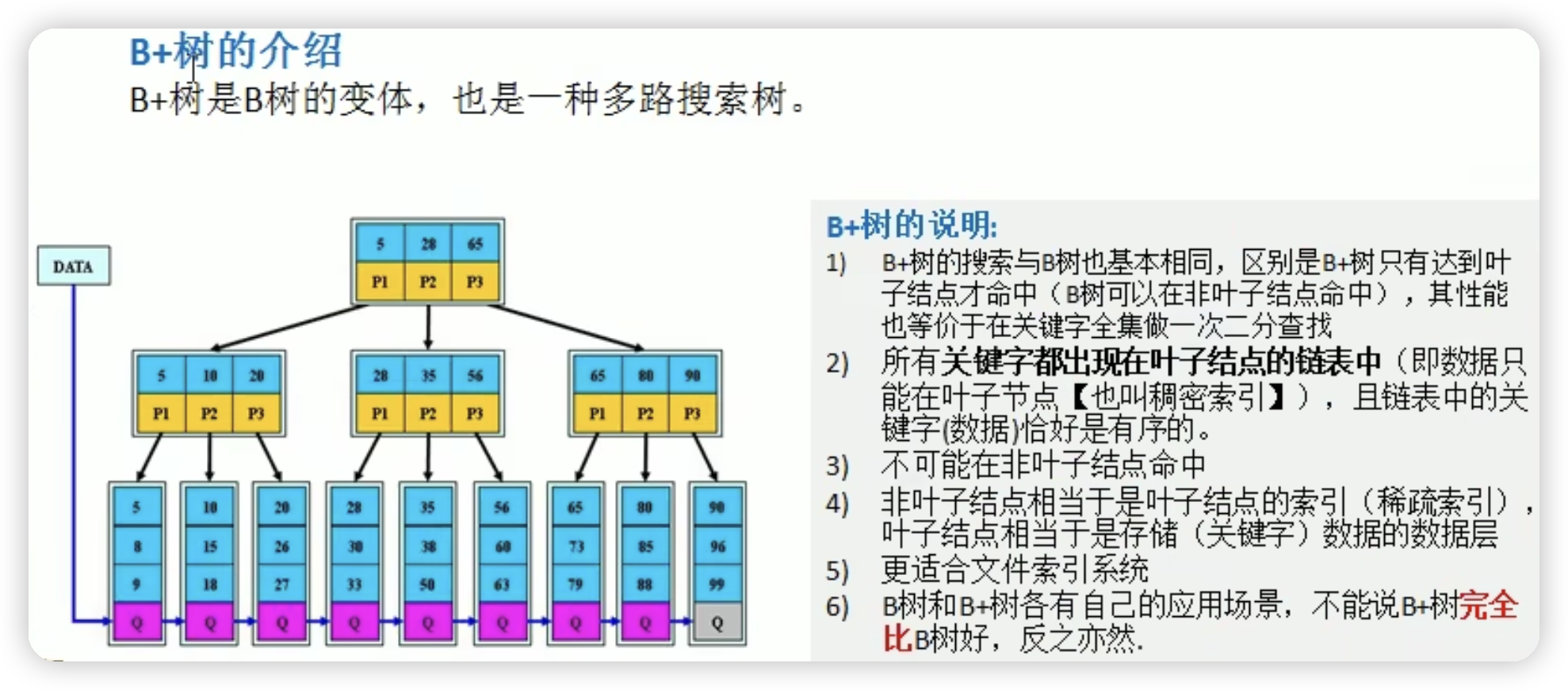
B+树
- 节点(Node):B+树的节点分为内部节点和叶子节点两种类型。每个节点包含键值对(Key-Value)和指向子节点的指针。在B+树中,节点的大小通常与磁盘页的大小相匹配,以便有效地利用磁盘读写。
- 链表(Linked List):B+树的叶子节点之间使用链表进行连接,以支持按顺序遍历和范围查询。链表中的每个节点包含键值对和指向下一个叶子节点的指针。
B*树
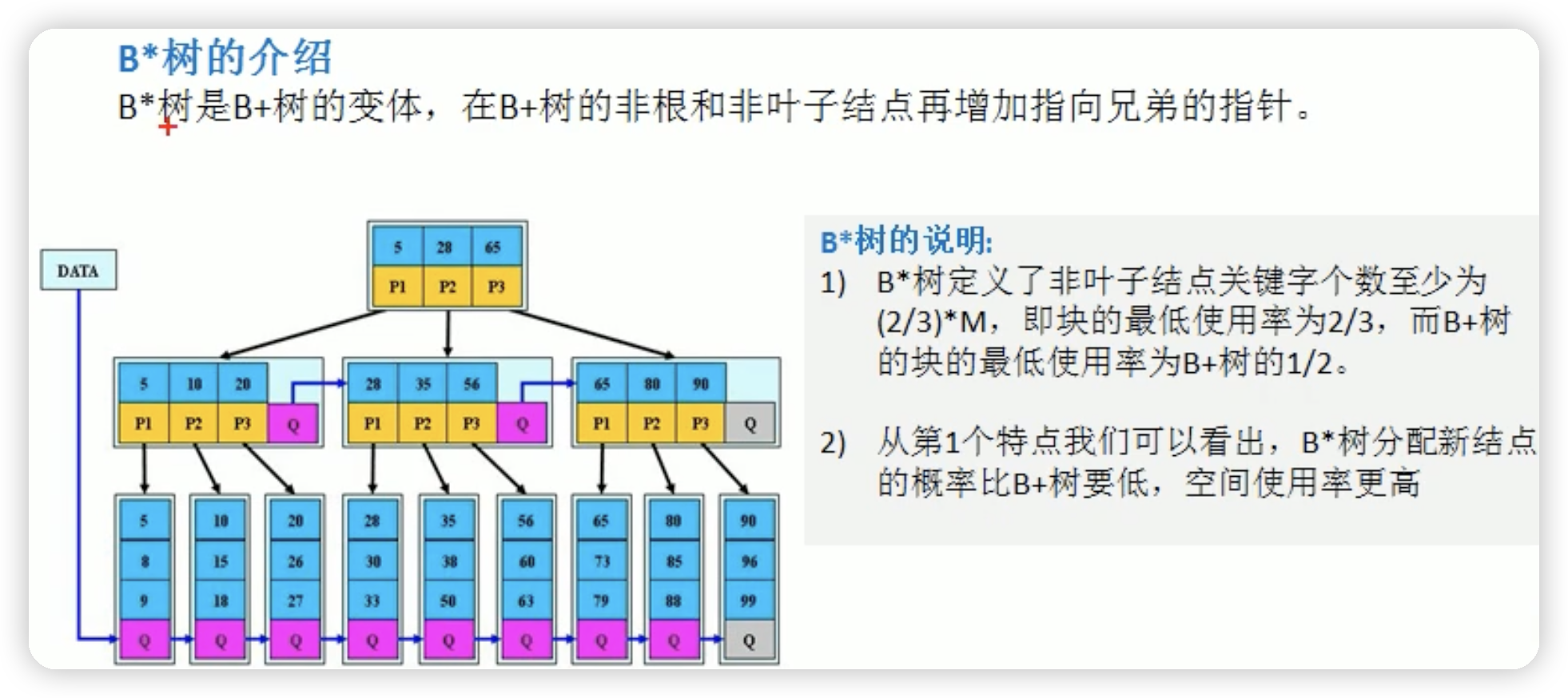
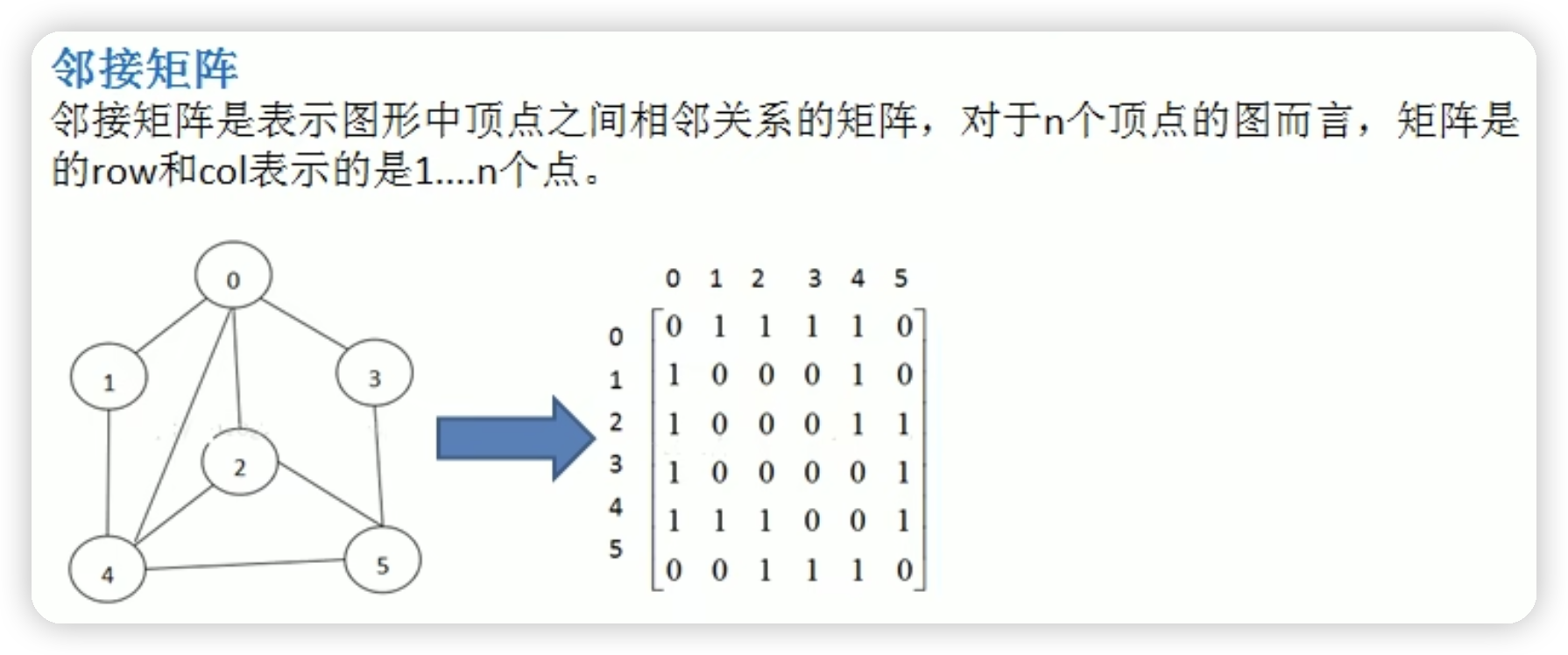
图
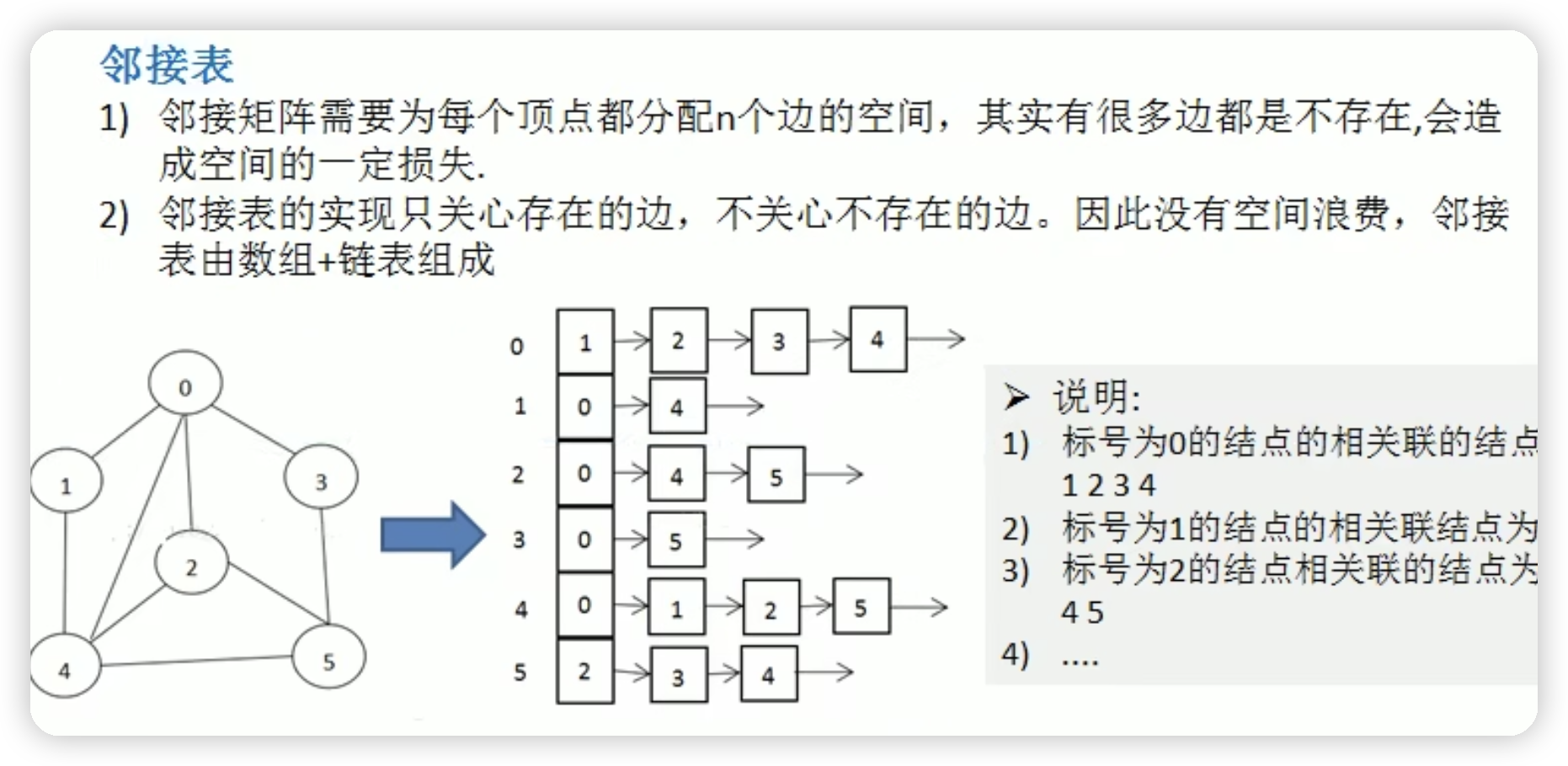
DFS
利用dfs遍历图中所有节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
package graph;
import java.util.ArrayList;
public class graph {
//存储邻接矩阵
private int[][]edges;
//表示边的数量
private int num;
//设置访问矩阵
boolean []visited;
public static void main(String[] args) {
graph g = new graph(4);
g.insertEdge(0, 1,1);
g.insertEdge(0, 2,1);
g.insertEdge(1, 2,1);
g.insertEdge(2, 0,1);
g.insertEdge(2, 3,1);
g.insertEdge(3, 3,1);
g.DFS();
}
public graph(int n){
edges=new int[n][n];
num=0;
visited=new boolean[n];
}
//添加边
public void insertEdge(int v1,int v2,int weight){
edges[v1][v2]=weight;
edges[v2][v1]=weight;
num++;
}
public int getEdgenum(){
return num;
}
//找到第一个邻接点
public int getFirstVex(int index){
for(int i=0;i<edges[0].length;i++){
if(edges[index][i]>0){
return i;
}
}
return -1;
}
//找到下一个邻接点
public int getNextVetex(int v1,int v2){
for(int i=v2+1;i<edges[0].length;i++){
if(edges[v1][i]>0){
return i;
}
}
return -1;
}
//开始dfs遍历
public void dfs(int v,boolean []visited){
System.out.println(v+" ");
visited[v]=true;
int v2=getFirstVex(v);
while(v2!=-1){
if(!visited[v2])
dfs(v2,visited);
v2=getNextVetex(v,v2);
}
}
public void DFS(){
for(int i=0;i<edges.length;i++){
if(!visited[i])
dfs(i,visited);
}
}
}
BFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public void BFS(){
LinkedList<Integer> queue=new LinkedList();
queue.add(0);
visited[0]=true;
while(!queue.isEmpty()){
int index=queue.pop();
System.out.print(index+" ");
for(int i=0;i<edges.length;i++){
if(edges[index][i]>0&&!visited[i]){
queue.add(i);
visited[i]=true;
}
}
}
}
经典算法
二分查找算法
非递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static int BinarySearch_no_recursion(int []array,int val){
int left=0;
int right=array.length-1;
while(left<=right){
int mid=(left+right)/2;
if(array[mid]>val)
right=mid-1;
else if(array[mid]<val)
left=mid+1;
else
return mid;
}
return -1;
}
递归
1
2
3
4
5
6
7
8
9
10
11
12
public static int BinarySearch_recursion(int []array,int val,int left,int right){
if(left<=right){
int mid=(left+right)/2;
if(array[mid]<val)
return BinarySearch_recursion(array,val,mid+1,right);
else if(array[mid]>val)
return BinarySearch_recursion(array,val,left,mid-1);
else
return mid;
}
return -1;
}
汉诺塔
1
2
3
4
5
6
7
8
9
10
11
12
public static void Hanoitower(int num,char a,char b,char c){
if(num==1){
System.out.println("第1个盘"+a+"->"+c);
}else {
//先把上面的n-1从a盘通过c盘的帮助放到b盘
Hanoitower(num-1,a,c,b);
//再把最后一个从a盘拿到c盘
System.out.println("第"+num+"个盘"+a+"->"+c);
//再把n-1盘从b盘通过a盘放到c盘
Hanoitower(num-1,b,a,c);
}
}
动态规划
- 定义状态:首先要明确问题的状态,即要解决的子问题中变化的量。每个子问题需要表示为一个状态,这些状态通常由问题的输入参数确定。
- 定义状态转移方程:通过观察问题,我们可以找到子问题之间的关联性,从而建立状态转移方程。状态转移方程表示当前状态与前一状态之间的关系。
- 初始化:确定最简单的问题的解,并初始化对应的状态。
- 确定计算顺序:根据状态转移方程,确定计算状态的顺序。一般来说,我们可以从最小的子问题开始计算,逐步向大问题扩展,确保每个子问题的解都已经计算过。
- 计算最优解:根据状态转移方程,依次计算每个子问题的解,并保存起来供后续使用。
- 提取最优解:根据问题的具体要求,从计算得到的状态中提取出最终的最优解
背包问题

01背包问题
1
2
3
4
5
6
7
8
9
10
11
12
13
public static int pack01(int []weight,int []values,int capacity){
int [][]dp=new int[weight.length+1][capacity+1];
for(int i=1;i<=weight.length;i++){
for (int j=1;j<= capacity;j++){
if(weight[i-1]>j)
dp[i][j]=dp[i-1][j];
else
//因为dp数组在两个维度上多扩充了一组,所以dp数组的i 相当于weight和values数组的i-1
dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-weight[i-1]]+values[i-1]);
}
}
return dp[weight.length][capacity];
}
完全背包问题
完全背包问题相较于01背包,区别在于物品的数量是无限的,所以是从同一行的减去对应容量的dp然后再加上一个value
1
2
3
4
5
6
7
8
9
10
11
public static int pack_comp(int[]weights,int []values,int capacity){
int [][]dp=new int[weights.length+1][capacity+1];
for(int i=1;i<=weights.length;i++)
for(int j=1;j<=capacity;j++){
if(weights[i-1]>j)
dp[i][j]=dp[i-1][j];
else
dp[i][j]=Math.max(dp[i-1][j],dp[i][j-weights[i-1]]+values[i-1]);
}
return dp[weights.length][capacity];
}
多重背包问题
使用第三个for循环的意思是将这一个物品在某个容量的时候进行多次比较,选出当前容量下数量最合适的结果
1
2
3
4
5
6
7
8
9
10
11
public static int pack_multiple(int []weights,int []values,int []counts,int capacity){
int [][]dp=new int[weights.length+1][capacity+1];
for(int i=1;i<=weights.length;i++)
for(int j=1;j<=capacity;j++){
dp[i][j]=dp[i-1][j];
for(int k=1;k<counts[i-1]&&k*weights[i-1]<=j;k++){
dp[i][j]=Math.max(dp[i][j],dp[i-1][j-k*weights[i-1]]+values[i-1]*k);
}
}
return dp[weights.length][capacity];
}
BF
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static int BF(String text,String str){
if(text==null||str==null||text.length()==0||str.length()==0)
return -1;
int i=0;int j=0;
while(i<text.length()&&j<str.length()){
if(text.charAt(i)==str.charAt(j)){
i++;j++;
}else{
i=i-j+1;
j=0;
}
}
if(j==str.length())
return i-j;
else
return -1;
}
KMP
求next数组时,k的位置一直都是从头多少个后面是匹配的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
package Algorithm;
public class kmpDemo {
public static void main(String[] args) {
String text = "ABABDABACDABABCABAB";
String pattern = "ABABCABAB";
int []next=new int[pattern.length()+1];
int res=kmp(next,pattern,text);
System.out.println(res);
}
public static int kmp(int []next,String str,String S){
if(str==null||S==null||str.length()==0||S.length()==0)
return -1;
int i=0,j=0;
getNext(next,str);
while(i<str.length()&&j<S.length()){
if(i==-1||str.charAt(i)==S.charAt(j)){
i++;
j++;
}else {
i=next[i];
}
}
if(i==str.length())
return j-str.length();
else
return -1;
}
public static void getNext(int []next,String str){
next[0]=-1;next[1]=0;
int k=0;
for(int i=1;i<str.length();i++){
//k=-1表示全新的字符,或者是找到相同的字符,这两种情况就可以写入next数组了
if(k==-1||str.charAt(k)==str.charAt(i)){
next[i]=k+1;
k++;
}
//表示没找到 但还没找完 继续往前找 用next是因为
else{
k=next[k];
}
}
}
}
贪心算法
集合覆盖问题
主要思路是将当前覆盖数量最多的集合加入,然后删除已经覆盖过的元素,然后再进行比较,找到目前覆盖最多的集合再加入,直到全部覆盖
1
2
retainAll会将temp中所以不在all里面的都删除
temp.retainAll(all);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
package Algorithm;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.HashSet;
import java.util.Map;
public class greedyDemo {
public static void main(String[] args) {
HashMap<String, HashSet<String>>broadcast=new HashMap<>();
HashSet<String>hashSet1=new HashSet<>();
hashSet1.add("bj");
hashSet1.add("sh");
hashSet1.add("tj");
HashSet<String>hashSet2=new HashSet<>();
hashSet2.add("gz");
hashSet2.add("bj");
hashSet2.add("sz");
HashSet<String>hashSet3=new HashSet<>();
hashSet3.add("cd");
hashSet3.add("sh");
hashSet3.add("hz");
HashSet<String>hashSet4=new HashSet<>();
hashSet4.add("tj");
hashSet4.add("sh");
HashSet<String>hashSet5=new HashSet<>();
hashSet5.add("hz");
hashSet5.add("dl");
broadcast.put("k1",hashSet1);
broadcast.put("k2",hashSet2);
broadcast.put("k3",hashSet3);
broadcast.put("k4",hashSet4);
broadcast.put("k5",hashSet5);
HashSet<String>all=new HashSet<>();
for(Map.Entry<String,HashSet<String>>entry:broadcast.entrySet()){
for(String city:entry.getValue()){
all.add(city);
}
}
//存放选择的电台
ArrayList<String>arrayList=new ArrayList<>();
//定义一个hashset来临时存放
HashSet<String>temp=new HashSet<>();
String maxKey=null;
while(all.size()!=0){
for(Map.Entry<String,HashSet<String>>entry:broadcast.entrySet()){
temp.addAll(entry.getValue());
//retainAll会将temp中所以不在all里面的都删除
temp.retainAll(all);
if(temp.size()>0&&(maxKey==null||temp.size()>broadcast.get(maxKey).size())){
maxKey=entry.getKey();
}
temp.clear();
}
arrayList.add(maxKey);
all.removeAll(broadcast.get(maxKey));
maxKey=null;
}
System.out.print(arrayList.toString());
}
}
最小生成树
prim
选点


这种解法的思路很简单,每次遍历整张图 找到一个节点是x坐标已经访问过的,y坐标没有访问过,并且是最小值的点 不过缺点就是时间复杂度太高
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
private static int prim(int [][]graph,Character []data,int v){
int []visited=new int[graph.length];
visited[v]=1;
//记录两个顶点的下标
int h1=-1;
int sum=0;
ArrayList<Character>arrayList=new ArrayList<>();
arrayList.add(data[v]);
for(int k=1;k<graph.length;k++){
int minWeight=Integer.MAX_VALUE;
for(int i=0;i<graph.length;i++){
for(int j=0;j<graph[0].length;j++){
if(visited[i]==1&&visited[j]==0&&graph[i][j]!=0&&graph[i][j]<minWeight){
minWeight=graph[i][j];
h1=j;
}
}
}
visited[h1]=1;
sum+=minWeight;
arrayList.add(data[h1]);
}
return sum;
}
第二种解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
import java.util.Arrays;
public class PrimMST {
private static final int V = 5; // 图的顶点数
// 用于找到具有最小键值且尚未包括在 MST 中的顶点
private int minKey(int[] key, boolean[] mstSet) {
int min = Integer.MAX_VALUE, minIndex = -1;
for (int v = 0; v < V; v++) {
if (!mstSet[v] && key[v] < min) {
min = key[v];
minIndex = v;
}
}
return minIndex;
}
private void primMST(int graph[][]) {
int parent[] = new int[V]; // 存储最小生成树
int key[] = new int[V]; // 存储键值,用于选择下一个顶点
boolean mstSet[] = new boolean[V]; // 标记顶点是否已包括在 MST 中
Arrays.fill(key, Integer.MAX_VALUE);
Arrays.fill(mstSet, false);
key[0] = 0; // 从第一个顶点开始构建 MST
parent[0] = -1;
for (int count = 0; count < V - 1; count++) {
int u = minKey(key, mstSet);
mstSet[u] = true;
for (int v = 0; v < V; v++) {
if (graph[u][v] != 0 && !mstSet[v] && graph[u][v] < key[v]) {
parent[v] = u;
key[v] = graph[u][v];
}
}
}
// 打印最小生成树
System.out.println("Edge \t Weight");
for (int i = 1; i < V; i++) {
System.out.println(parent[i] + " - " + i + "\t" + graph[i][parent[i]]);
}
}
}
kruskal
选边


对于问题二的思路是将已经加入的点放入集合中,将每个点的终点加入集合中,终点指的是在连通的情况下能到的最大的点,判断一条线的加入是否会形成回路是判断这条线的两个点是否有相同的终点,如果有相同的终点说明这条线的两个点一定能和终点形成回路
这个代码的思路是找当前图中最小的边并且边的两个节点不属于一类,找到之后记录下来,将这两个节点设置为一类
设置一类的方法是设置一个parent数组,表示了每一个节点的根节点,刚开始为自己,然后如果要设置一类,就将一个点的根节点设置为一个点的根节点的子节点,这样通过递归查找,两个点就拥有了通向的根节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
package Algorithm;
public class kruskalDemo {
private int V; // 顶点数
private int[][] graph; // 邻接矩阵
private int numEdges; // 边的数量
public kruskalDemo(int v){
V = v;
graph = new int[V][V];
numEdges = 0;
}
public void addEdge(int src, int dest, int weight) {
graph[src][dest] = weight;
graph[dest][src] = weight;
numEdges++;
}
//父亲节点一定是一个点等于值的存在,最开始都是一个个根节点,然后通过union 将一部分节点的根节点设置其他节点根节点的子节点
public int find(int []parent,int i){
if(parent[i]==i)
return i;
return find(parent,parent[i]);
}
//将x的根节点设置为y的根节点的子节点 这样查找其他 这两个就有相同的根节点 就是一类了 属于一类的点 表示都能到同一个点
// 而kruskal算法找回路的时候就是需要判断两个节点是否有相同的终点
public void union(int []parent,int x,int y){
int parx=find(parent,x);
int pary=find(parent,y);
parent[parx]=pary;
}
public void kruskal(){
int []parent=new int[V];
int [][]res=new int[V-1][3];
for(int i=0;i<parent.length;i++){
parent[i]=i;
}
int count=0;
while(count<V-1){
int min=Integer.MAX_VALUE;
int src=-1;int dest=-1;
for(int i=0;i<V;i++){
for(int j=0;j<V;j++){
if(graph[i][j]!=0&&find(parent,i)!=find(parent,j)&&graph[i][j]<min){
src=i;
dest=j;
min=graph[i][j];
}
}
}
//这个判断表示进入过if 那么取得的边是满足条件的 防止出现不成树 边缺失等情况
if(src!=-1&&dest!=-1){
res[count][0]=src;
res[count][1]=dest;
res[count][2]=min;
union(parent,src,dest);
count++;
}
}
for(int i=0;i<res.length;i++){
System.out.println(res[i][0]+" "+res[i][1]+" "+res[i][2]+" ");
}
}
public static void main(String[] args) {
int V = 4; // 顶点数
kruskalDemo graph = new kruskalDemo(V);
graph.addEdge(0, 1, 10);
graph.addEdge(0, 2, 6);
graph.addEdge(0, 3, 5);
graph.addEdge(1, 3, 15);
graph.addEdge(2, 3, 4);
graph.kruskal();
}
}
最短距离
Dijkstra
Dijkstra算法适用于带有非负权重的图,但不适用于包含负权边的图。如果有负权边,应该使用其他算法,如Bellman-Ford算法
主要思路是从起始顶点开始,逐渐找到离起始顶点最近的顶点,然后加入distance数组中,然后通过对
1
distance[min]+graph[min][j]<distance[j]
通过对这个语句的判断来逐渐找到到达各个顶点的最小距离

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
package Algorithm;
import java.util.Arrays;
public class DijsktraDemo {
private int V;
private int [][]graph;
public static void main(String[] args) {
int V = 6; // 顶点数
DijsktraDemo graph = new DijsktraDemo(V);
graph.addEdge(0, 1, 4);
graph.addEdge(0, 2, 2);
graph.addEdge(1, 2, 5);
graph.addEdge(1, 3, 10);
graph.addEdge(2, 4, 3);
graph.addEdge(3, 4, 7);
graph.addEdge(3, 5, 5);
graph.addEdge(4, 5, 2);
int startVertex = 0; // 起始顶点
graph.dijkstra(startVertex);
}
private DijsktraDemo(int V){
this.V=V;
graph=new int[V][V];
}
private void addEdge(int i,int j,int weight){
graph[i][j]=weight;
graph[j][i]=weight;
}
private void dijkstra(int startVertex){
//表示已经计算过的最短边的点,就不再进行比较了
boolean []visited=new boolean[V];
//表示每个点到起始点的最短距离
int []distance=new int[V];
Arrays.fill(distance,Integer.MAX_VALUE);
//到自己的最短距离为0
distance[startVertex]=0;
for(int i=0;i<V-1;i++){
//找到当前没有访问过的,最短距离的点
int minVertex=findMin(distance,visited);
//这个点已经是最短距离了,表示已经加入了 然后通过他对其他没访问过的点进行最短距离更新
visited[minVertex]=true;
for(int j=0;j<V;j++){
if(!visited[j]&&graph[minVertex][j]!=0&&distance[minVertex]!=Integer.MAX_VALUE&&distance[minVertex]+graph[minVertex][j]<distance[j]){
distance[j]=distance[minVertex]+graph[minVertex][j];
}
}
}
System.out.println(Arrays.toString(distance));;
}
private int findMin(int []distance,boolean []visited){
int min=Integer.MAX_VALUE;
int minVertex=-1;
for(int i=0;i<V;i++){
if(!visited[i]&&distance[i]<min){
minVertex=i;
min=distance[i];
}
}
return minVertex;
}
}
Floyd

主要思路是利用一个三重for循环设置一个中间节点k,然后对整个表的其他所有节点进行判断,进行节点的更新
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
package Algorithm;
import java.util.Arrays;
public class floydDemo {
private int V;
private int[][]graph;
public static void main(String[] args) {
int V = 4; // 顶点数
floydDemo graph = new floydDemo(V);
int[][] edges =
{0, 1, 3},
{0, 3, 7},
{1, 2, 1},
{2, 3, 2}
;
for (int[] edge : edges) {
graph.addEdge(edge[0], edge[1], edge[2]);
}
graph.floyd();
}
floydDemo(int V){
this.V=V;
graph=new int[V][V];
}
private void addEdge(int i,int j,int weight){
graph[i][j]=weight;
graph[j][i]=weight;
}
private void floyd(){
int [][]distance=new int[V][V];
for(int i=0;i<V;i++){
for(int j=0;j<V;j++){
if(i==j)
distance[i][j]=0;
else if(graph[i][j]!=0)
distance[i][j]=graph[i][j];
else
distance[i][j]=Integer.MAX_VALUE;
}
}
//以k为中间节点 i为出发节点 j为终止节点 逐个进行判断更新
for(int k=0;k<V;k++)
for(int i=0;i<V;i++)
for(int j=0;j<V;j++)
if(distance[i][k]!=Integer.MAX_VALUE&&distance[k][j]!=Integer.MAX_VALUE&&distance[i][k]+distance[k][j]<distance[i][j]){
distance[i][j]=distance[i][k]+distance[k][j];
}
for(int []dis:distance)
System.out.println(Arrays.toString(dis));
}
}
骑士周游问题
和迷宫dfs问题一样
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
package Algorithm;
import java.util.Arrays;
import java.util.Stack;
public class KnightsTourDemo {
private int width;
private int high;
private int start_x;
private int start_y;
private int count;
private int [][]visited;
public static void main(String[] args) {
KnightsTourDemo knightsTourDemo=new KnightsTourDemo(8,8,0,0);
knightsTourDemo.KnightsTour();
System.out.println(knightsTourDemo.count);
for(int []vis: knightsTourDemo.visited){
System.out.println(Arrays.toString(vis));
}
}
KnightsTourDemo(int width,int high,int start_x,int start_y){
this.width=width;
this.high=high;
this.start_x=start_x;
this.start_y=start_y;
visited=new int[high][width];
}
private Boolean KnightsTour(){
int [][]moves=
{2, 1}, {1, 2}, {-1, 2}, {-2, 1}, {-2, -1}, {-1, -2}, {1, -2}, {2, -1};
count=1;
Stack<Integer>stack=new Stack<>();
stack.push(start_x);stack.push(start_y);
while(!stack.isEmpty()){
boolean flag=false;
if(count==high*width){
return true;
}
int y=stack.pop();
int x=stack.pop();
visited[x][y]=1;
stack.push(x);stack.push(y);
for(int []move:moves){
int i=x+move[0];
int j=y+move[1];
if(i>=0&&i<high&&j>=0&&j<width&&visited[i][j]!=1){
count++;
stack.push(i);
stack.push(j);
flag=true;
break;
}
}
if(!flag){
stack.pop();
stack.pop();
}
}
return false;
}
}
也可以用bfs进行遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
private boolean bfs(){
int [][]moves=
{2, 1}, {1, 2}, {-1, 2}, {-2, 1}, {-2, -1}, {-1, -2}, {1, -2}, {2, -1};
count=1;
Queue<Integer> list=new LinkedList<>();
list.add(start_x);list.add(start_y);
visited[start_x][start_y]=1;
while(!list.isEmpty()){
int x=list.poll();
int y=list.poll();
for(int []move:moves){
int i=x+move[0];
int j=y+move[1];
if(i>=0&&i<high&&j>=0&&j<width&&visited[i][j]!=1){
count++;
visited[i][j]=1;
list.add(i);
list.add(j);
}
}
}
if(count==high*width){
return true;
}else {
return false;
}
}